Gottfried Wilhelm von Leibniz - Metodo matematico e calcolo simbolico

1) Introduzione
2) Lettura
3) Guida alla lettura
4) Guida alla Comprensione
Introduzione
Il primo documento menzionato, "Il vero metodo" datato 1677, risale al periodo in cui Leibniz viveva a Hannover. In quel tempo, mentre si dedicava a varie attività tecniche, si immerse nello studio di diverse questioni teoriche. Tra queste, emergeva il suo interesse per lo sviluppo di una lingua universale. Questa lingua sarebbe stata formata da "caratteri" con un significato preciso e unico, che avrebbero permesso di trattare le idee con un metodo di calcolo simile a quello utilizzato in matematica, garantendo maggiore chiarezza e velocità di elaborazione. Questa concezione di un calcolo delle idee era legata all'idea di creare una struttura enciclopedica della conoscenza e di un alfabeto del pensiero. Vi è anche un estratto di una lettera inviata a Elisabetta, badessa di Herford, in cui Leibniz descrive il principio di questa visione, basato sulla necessità di dare una "forma" alle dichiarazioni scientifiche, così che il loro valore possa essere determinato e quantificato.
Lettura
Il vero metodo
Il vero metodo, preso in tutta la sua estensione, è cosa sinora affatto ignota, a mio parere, e non lo si è praticato se non nelle matematiche. Nelle matematiche stesse è ancora molto imperfetto, come ho avuto la fortuna di far vedere ad alcuni (che al giorno d'oggi sono annoverati tra i primi matematici del secolo) con prove sorprendenti. E spero di darne dei saggi, che forse non saranno indegni della posterità.
Tuttavia, se il metodo dei matematici non è stato sufficiente per trovare tutto ciò che si poteva desiderare da loro, è stato quantomeno capace di garantirli dagli errori e, se non hanno detto tutto ciò che dovevano, non hanno neppur detto ciò che non avrebbero dovuto.
Se coloro che hanno coltivato le altre scienze avessero imitato almeno in questo punto i matematici, saremmo molto felici: avremmo da tempo una metafisica certa, come sarebbe certa la morale che ne dipende; perché la metafisica racchiude la conoscenza di Dio e dell'anima, che deve regolare la nostra vita. [...] Ora, la ragione per cui l'arte di dimostrare non si trova sinora se non nelle matematiche non è stata ben penetrata da nessuno, perché se si fosse conosciuta la causa del male, da un pezzo si sarebbe anche trovato il rimedio. [...]
Si tratta di un male non privo di rimedio, benché in prima istanza ci sembri che non ve ne sia. Ma chi vorrà considerare quanto sto per dire, cambierà presto parere. Bisogna dunque notare che le prove o esperienze che si fanno in matematica per garantirsi contro un falso ragionamento (come sono la prova del nove, il calcolo di Ludolph van Ceulen intorno alla dimensione del cerchio, le tavole trigonometriche, e altre) non si svolgono sulla cosa stessa, ma su caratteri che abbiamo sostituito al posto della cosa. [...]
Ma la prova non si compie che sulla carta e, di conseguenza, sui caratteri che rappresentano la cosa e non sulla cosa stessa. [...] Ne risulta chiaro che se si potessero trovare dei caratteri o segni propri a esprimere tutti i nostri pensieri tanto nitidamente ed esattamente quanto l'aritmetica esprime i numeri o l'analisi geometrica esprime le linee, si potrebbe fare in tutte le materie, in quanto sono sottoposte al ragionamento, tutto quel che si può fare in aritmetica e geometria.
Perché tutte le ricerche che dipendono dal ragionamento si farebbero mediante la trasposizione di questi caratteri e mediante una specie di calcolo, il che renderebbe agevolissima l'invenzione di belle cose. Perché non occorrerebbe rompersi la testa come si è costretti a fare oggi e, nondimeno, si sarebbe certi di poter fare tutto ciò che ex datis sarebbe fattibile.
In più si farebbe convenire tutti quanti su ciò che si fosse trovato o concluso, perché sarebbe facile verificare il calcolo sia ripetendolo, sia sviluppando qualche prova simile a quella del nove in aritmetica. E se qualcuno dubitasse di ciò che io avessi presentato, gli direi: «Signore, contiamo». E così, presi penna e inchiostro, ci toglieremmo presto dall'impiccio.
Aggiungo sempre: «in quanto si può fare mediante il ragionamento, ex datis». Perché sebbene occorrano sempre certe esperienze per servire di base al ragionamento, una volta che le esperienze siano date, se ne trarrebbe sempre tutto ciò che chiunque altro sarebbe mai capace di ricavarne e si scoprirebbero persino quelle che resterebbero ancora da fare, per chiarire tutti i dubbi rimasti. Sarebbe un ausilio mirabile persino in politica e in medicina, per ragionare in modo costante e perfetto sui sintomi e sulle circostanze date. Perché quand'anche non si avessero sufficienti circostanze date per formare un giudizio infallibile, si potrebbe sempre determinare che cosa è più probabile ex datis. Ed ecco tutto ciò che la ragione può fare.
Ora i caratteri che esprimeranno tutti i nostri pensieri comporranno una nuova lingua, che potrà essere scritta e pronunciata: questa lingua sarà molto difficile a farsi, ma molto facile da apprendere. Sarà ben presto accettata da tutti, a causa del suo grande uso e della sua sorprendente facilità. Servirà meravigliosamente alla comunicazione tra popoli diversi, che aiuterà a farla accogliere. Chi scriverà in questa lingua non si ingannerà, purché eviti gli errori di calcolo e i barbarismi, i solecismi e altri errori di grammatica e di costruzione.
In più questa lingua avrà una proprietà meravigliosa, che è di chiudere la bocca agli ignoranti. Perché in questa lingua non si potrà parlare né scrivere se non di ciò che si comprende; oppure, se si oserà farlo, delle due l'una: o la vanità di ciò che si accampa sarà evidente a tutti, o si imparerà scrivendo, o parlando. Come, in effetti, chi calcola impara scrivendo e chi parla, a volte, ha delle uscite a cui non pensava, lingua praecurrente mentem. Il che accadrà soprattutto in questa lingua, a causa della sua esattezza, in quanto non vi saranno né equivoci né anfibologie, e tutto ciò che vi si dirà in modo intelligibile, sarà detto a proposito. [...]
L'importanza della forma
In una parola, si tratta di non fare degli argomenti se non in forma. Mi sembra già di vedere la gente che si sbraccia contro di me e mi rimanda alla scolastica. Ma li prego di portare un po' di pazienza, perché forse non mi intendono bene: gli argomenti in forma non sono tutti distinti col marchio del Barbara Celarent. Ogni dimostrazione rigorosa, che non ometta nulla di necessario alla forza del ragionamento, è in quel novero, e oso dire che il conteggio di un esattore, oppure un calcolo analitico, è un argomento in forma, poiché non vi manca nulla e poiché la forma o disposizione di tutto il ragionamento è la causa dell'evidenza. Non è che la forma, a distinguere un libro di conti tenuto secondo la pratica che si chiama comunemente italiana (sulla quale Stevin ha composto un intero trattato) dal giornale confuso di un qualche ignorante in materia di commercio.
Ecco perché sostengo che, al fine di ragionare ovunque con evidenza, bisogna osservare qualche formalità costante. Vi sarà meno eloquenza e più certezza. Ma per determinare questa forma, che nella metafisica, nella fisica e nella morale non darebbe minor esito di quanto il calcolo nella matematica, e che laddove non si può che ragionare verisimilmente, indicherebbe persino i gradi di probabilità, bisognerebbe presentare qui le riflessioni che ho fatto su una nuova caratteristica, il che sarebbe troppo lungo. Scomponibilità dei significati e trasformazione delle esperienze in dati calcolabili Dirò tuttavia in poche parole, che questa caratteristica rappresenterebbe veridicamente e distintamente i nostri pensieri; e quando un pensiero è composto di altri più semplici, il suo carattere lo sarebbe nello stesso modo. Non oso dire quel che ne risulterebbe per il perfezionamento delle scienze: parrebbe incredibile. E tuttavia ve n'è la dimostrazione. Dirò solamente che, poiché ciò che noi sappiamo è ragionamento o esperienza, è sicuro che ogni ragionamento in materie dimostrative o probabili, una volta fatto ciò, non richiederebbe maggiore abilità di un calcolo algebrico: vale a dire che si trarrebbe ex datis experimentis tutto ciò che se ne possa trarre, proprio come nell'algebra.
Guida alla lettura
1) Da che cosa dipende la chiarezza di una lingua fatta di caratteri?
La chiarezza di una lingua fatta di caratteri, come discusso da Leibniz nei testi che hai condiviso, dipende principalmente dalla capacità di questi caratteri di esprimere i concetti in modo nitido ed esatto. Leibniz sottolinea che se si potessero trovare caratteri o segni adeguati per esprimere tutti i nostri pensieri tanto chiaramente quanto l’aritmetica esprime i numeri o l’analisi geometrica esprime le linee, allora sarebbe possibile applicare un metodo di calcolo simile a quello usato in matematica a qualsiasi materia sottoposta al ragionamento.
Inoltre, secondo Leibniz, questa precisione nel linguaggio dei caratteri garantirebbe che tutte le ricerche che dipendono dal ragionamento si potrebbero svolgere mediante la trasposizione di questi caratteri e mediante un calcolo, facilitando enormemente la scoperta e l'invenzione di nuove conoscenze. La chiarezza e l'accuratezza di tali caratteri sarebbero quindi essenziali per assicurare che la lingua possa effettivamente funzionare come un mezzo di calcolo universale e inequivocabile per il ragionamento.
2) Elenca i vantaggi che Leibniz si aspetta dalla nuova lingua simbolica per chi la pratica e per la comunicazione.
Ecco un elenco dei vantaggi che Leibniz prevede dalla nuova lingua simbolica, basato sui brani che mi hai inviato:
Chiarezza e precisione nel ragionamento: La nuova lingua permetterebbe di esprimere i pensieri in modo nitido ed esatto, simile a come l'aritmetica rappresenta i numeri o come l'analisi geometrica rappresenta le linee. Questo porterebbe a un ragionamento più chiaro e preciso.
Facilità di verifica e consenso universale: Essendo basata su un calcolo simbolico, sarebbe facile verificare le conclusioni tramite semplici calcoli. Questo avrebbe il potenziale di unificare l'accordo su temi discussi, poiché le conclusioni potrebbero essere validate facilmente da chiunque.
Semplicità di apprendimento e utilizzo: Nonostante la complessità della sua creazione, una volta stabilita, questa lingua sarebbe facile da apprendere e da usare. Ciò avrebbe un impatto positivo sulla diffusione del sapere e sull'istruzione.
Comunicazione efficace tra culture diverse: La lingua aiuterebbe notevolmente la comunicazione tra popoli diversi, promuovendo così una migliore comprensione interculturale e potenzialmente riducendo i conflitti.
Riduzione degli errori e delle incomprensioni: Chi scrive in questa lingua sarebbe protetto da errori di calcolo e da imprecisioni linguistiche come barbarismi e solecismi, contribuendo a una comunicazione più efficace e precisa.
Esclusione dell'ignoranza: Nella nuova lingua, non sarebbe possibile parlare o scrivere senza una comprensione chiara di ciò che si sta discutendo. Questo impedirebbe la diffusione di informazioni false o ingannevoli e aumenterebbe il livello generale di comprensione e conoscenza.
Potenziamento del ragionamento e della scoperta scientifica: Facilitando la trasformazione delle esperienze in dati calcolabili, la lingua potrebbe accelerare notevolmente il progresso scientifico e tecnologico, permettendo scienziati e ricercatori di dedurre conclusioni valide da insiemi di dati in modo più efficiente.
In sintesi, Leibniz immagina una rivoluzione nella comunicazione e nel pensiero umano, guidata dalla creazione di una lingua che potrebbe portare a una conoscenza più accurata e universale.
Guida alla Comprensione
1) Spiega il procedimento di costruzione della nuova lingua, come elaborazione delle esperienze e delle conoscenze acquisite.
Il procedimento di costruzione della nuova lingua proposto da Leibniz, come descritto nei passaggi del testo che hai condiviso, si fonda su alcuni principi chiave che riguardano l'elaborazione delle esperienze e delle conoscenze acquisite.
Uso di caratteri o segni univoci: Leibniz propone l'adozione di caratteri o segni che siano capaci di esprimere i pensieri con precisione ed esattezza, simili a come i numeri sono usati in aritmetica e le linee in geometria. Questi caratteri consentirebbero di rappresentare le idee in modo chiaro e diretto, riducendo le ambiguità.
Calcolo simbolico: Una volta definiti questi caratteri, si potrebbe utilizzare una specie di calcolo simbolico per manipolarli. Questo calcolo permetterebbe di effettuare ragionamenti complessi attraverso operazioni semplici sui segni, analogamente a quanto avviene nelle operazioni matematiche. L'idea è che, così come in matematica si utilizzano formule per risolvere problemi, anche nelle altre discipline si potrebbero usare formule basate su questi caratteri per trattare questioni teoriche.
Verifica e convalida delle idee: Con l'introduzione di questa lingua, ogni affermazione potrebbe essere verificata attraverso il calcolo. Se emergessero dubbi o disputazioni, si potrebbero risolvere "calcolando" nuovamente, garantendo così un metodo oggettivo e ripetibile per confermare la validità di un'idea o di una teoria.
Universalità e accessibilità: La lingua ideata da Leibniz sarebbe accessibile e facilmente apprendibile da tutti, grazie alla sua struttura logica e chiara. Ciò faciliterebbe la comunicazione tra persone di diverse culture e lingue, promuovendo una più ampia diffusione del sapere.
Formalizzazione delle esperienze: Le esperienze, trasformate in dati calcolabili attraverso questa lingua, potrebbero essere utilizzate come base per ulteriori ragionamenti. Una volta che le esperienze diventano dati formalizzati, potrebbero essere elaborate sistematicamente per derivarne nuove conoscenze.
In sintesi, la costruzione della nuova lingua descritta da Leibniz si basa sull'idea di creare un sistema universale di segni che permetta di trasformare ogni esperienza e conoscenza in dati formalizzati, suscettibili di essere elaborati attraverso un calcolo simbolico. Questo renderebbe il processo di ragionamento più rapido, preciso e verificabile, estendendo i benefici del metodo matematico a tutte le aree del sapere.
2) Perché una lingua simbolica permetterebbe di organizzare meglio il ragionamento ex datis (a partire dai dati)?
La proposta di Leibniz di una lingua simbolica, come descritto nei testi che hai fornito, mira a creare un sistema in cui ogni concetto, pensiero o processo logico sia espresso attraverso caratteri o segni specifici e univoci. Questa approccio promuove una serie di vantaggi nell'organizzazione e nel trattamento dei dati per ragionamento:
Precisione e chiarezza: Una lingua simbolica, essendo costituita da caratteri specifici per esprimere concetti, riduce ambiguità e imprecisioni. Le idee possono essere rappresentate in modo chiaro e diretto, similmente a come i numeri e le operazioni matematiche esprimono quantità e relazioni precise in aritmetica.
Calcolabilità: Utilizzando simboli specifici, il ragionamento può essere trasformato in una serie di operazioni simili a calcoli, permettendo di applicare metodi matematici per dedurre nuove informazioni o verificare l'accuratezza di una conclusione. Questo approccio rende il processo di deduzione più sistematico e meno soggetto a errori di logica.
Riproducibilità e verificabilità: Analogamente a come in matematica si può verificare un risultato ripetendo il calcolo, una lingua simbolica permette di verificare le conclusioni mediante "calcoli" analoghi. Se qualcuno ha dubbi su una conclusione, può semplicemente "ricontare" o rieseguire il calcolo simbolico per confermare o confutare il risultato.
Universalità e comunicabilità: Una lingua basata su simboli univoci e ben definiti sarebbe meno soggetta a malinterpretazioni e potrebbe essere compresa universalmente, superando le barriere linguistiche e culturali. Questo faciliterebbe la condivisione di conoscenze e idee tra diverse discipline e tra persone di diversi background.
Applicabilità estesa: Secondo Leibniz, questo metodo non solo sarebbe utile in matematica, ma potrebbe estendersi a quasi tutti i campi del sapere, compresi quelli meno esatti come la politica e la medicina, offrendo uno strumento per ragionare con maggiore certezza e precisione anche quando i dati disponibili sono incompleti o incerti.
In sintesi, una lingua simbolica, organizzando il pensiero in maniera precisa e calcolabile, potrebbe rivoluzionare il modo in cui ragioniamo e trattiamo le informazioni, rendendo il nostro pensiero più simile al metodo matematico in termini di precisione, efficienza e universalità.
3) Quali altri vantaggi scientifici deriverebbero dall'uso sistematico di una forma codificata? (Rispondi pensando alle esigenze di controllo della comunità scientifica).
L'uso di una forma codificata e sistematica per esprimere concetti scientifici, come suggerito da Leibniz, offrirebbe diversi vantaggi significativi per il controllo e l'avanzamento della scienza, in particolare nell'ambito della comunità scientifica:
Verificabilità e Ripetibilità: Utilizzando una forma codificata per rappresentare idee e processi scientifici, diventerebbe molto più semplice per altri scienziati verificare e ripetere esperimenti e calcoli. Leibniz immagina un sistema in cui, come in matematica, si possa facilmente ripetere un calcolo per confermarne l'esattezza, eliminando ambiguità e potenziali errori di interpretazione.
Comunicazione Universale: La creazione di una lingua universale per esprimere pensieri scientifici faciliterebbe enormemente la comunicazione tra scienziati di diverse discipline e culture. Questo migliorerebbe la collaborazione internazionale e accelererebbe il progresso scientifico attraverso una più efficiente condivisione delle conoscenze.
Riduzione degli Errori: Come Leibniz nota, chi scrive nella lingua codificata sarebbe protetto dagli errori di calcolo, barbarismi, solecismi e altri errori grammaticali che potrebbero altrimenti portare a conclusioni errate. Questo sistema aiuterebbe a mantenere un alto livello di precisione nelle pubblicazioni scientifiche.
Standardizzazione e Formalizzazione: L'adozione di una forma codificata standardizzerebbe le metodologie scientifiche, rendendo più sistematico il processo di ragionamento. Questo porterebbe a una maggiore chiarezza e comprensibilità delle ricerche scientifiche, con evidenti vantaggi per la formazione, la revisione e la valutazione peer-review.
Efficacia Educativa: Una lingua esatta e codificata per la scienza potrebbe migliorare significativamente l'efficacia dell'istruzione scientifica, riducendo il tempo necessario per apprendere complessi concetti scientifici e facilitando l'acquisizione di nuove conoscenze.
Incremento dell'Innovazione: Facilitando la manipolazione e il calcolo dei dati e delle idee, una forma codificata potrebbe portare a un aumento delle scoperte e delle innovazioni. La possibilità di "calcolare" conclusioni dai dati esistenti potrebbe rivelare nuove connessioni e intuizioni che altrimenti rimarrebbero occultate.
In sintesi, l'implementazione di una forma codificata per esprimere la scienza, come proposto da Leibniz, avrebbe il potenziale di rivoluzionare il modo in cui la conoscenza è acquisita, condivisa, e utilizzata nella comunità scientifica, portando a un'epoca di maggiore chiarezza, precisione, e collaborazione internazionale.
Fonti: Zanichetti, libri scolastici superiori

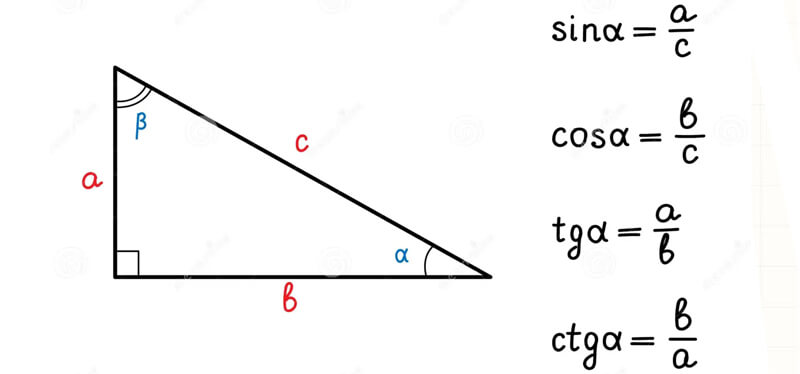 Identita trigonometriche - guida completa con esercizi risolti
Identita trigonometriche - guida completa con esercizi risolti
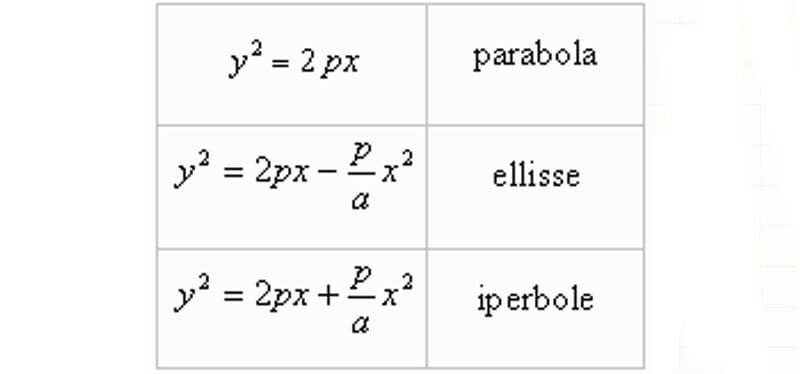 Equazione della parabola ellisse e iperbole - guida completa con esercizi risolti
Equazione della parabola ellisse e iperbole - guida completa con esercizi risolti
 Equazione della circonferenza - guida completa con esercizi risolti
Equazione della circonferenza - guida completa con esercizi risolti
 Logaritmi ed esponenziali - guida completa con esercizi risolti
Logaritmi ed esponenziali - guida completa con esercizi risolti
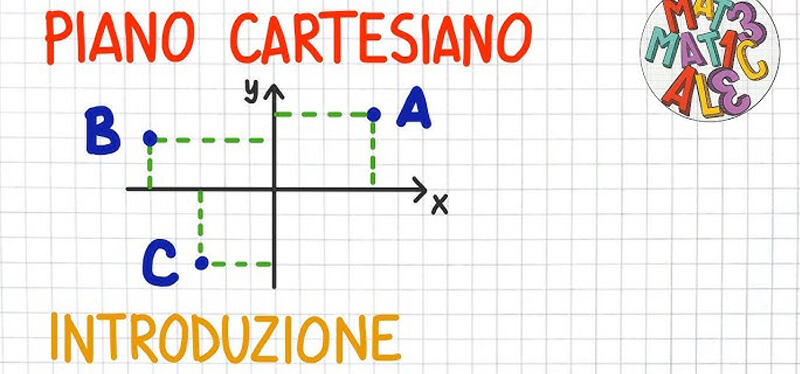 Il piano cartesiano - guida completa con esercizi risolti
Il piano cartesiano - guida completa con esercizi risolti
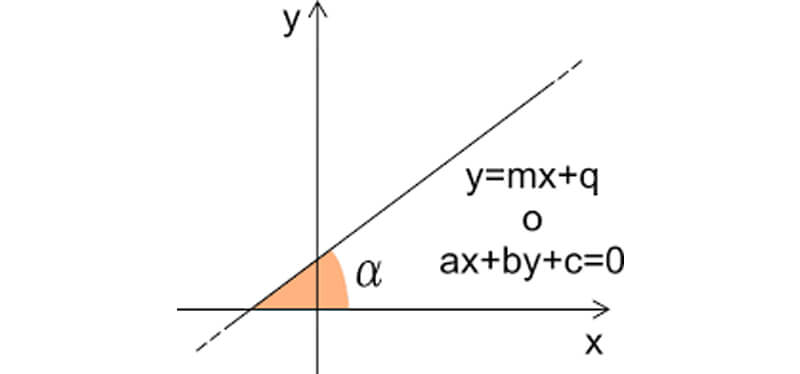 La retta - equazione e coefficiente angolare - guida completa con esercizi risolti
La retta - equazione e coefficiente angolare - guida completa con esercizi risolti
 Teorema dei seni e teorema del coseno - guida completa con esercizi risolti
Teorema dei seni e teorema del coseno - guida completa con esercizi risolti
 Seno coseno e tangente - guida completa con esercizi risolti
Seno coseno e tangente - guida completa con esercizi risolti
 Radicali e numeri complessi - guida completa con esercizi risolti
Radicali e numeri complessi - guida completa con esercizi risolti
 Guida completa alle disequazioni di secondo grado - teoria esercizi e approfondimenti
Guida completa alle disequazioni di secondo grado - teoria esercizi e approfondimenti
 Guida completa alle equazioni di secondo grado - teoria esercizi e aprofondimenti
Guida completa alle equazioni di secondo grado - teoria esercizi e aprofondimenti
 Guida completa al calcolo delle probabilita - teoria esercizi e approfondimenti
Guida completa al calcolo delle probabilita - teoria esercizi e approfondimenti
 Media moda e mediana - la statistica per tutti
Media moda e mediana - la statistica per tutti
 Le funzioni in matematica - guida completa con esercizi per tutti i livelli
Le funzioni in matematica - guida completa con esercizi per tutti i livelli
 Isometrie e similitudini - teoria esercizi e applicazioni
Isometrie e similitudini - teoria esercizi e applicazioni
 Introduzione alla geometria euclidea - teoria esercizi e approfondimenti
Introduzione alla geometria euclidea - teoria esercizi e approfondimenti
 Guida ai prodotti notevoli - teoria esercizi e applicazioni
Guida ai prodotti notevoli - teoria esercizi e applicazioni
 Alla scoperta delle disequazioni di primo grado - teoria ed esercizi
Alla scoperta delle disequazioni di primo grado - teoria ed esercizi
 Alla scoperta delle equazioni di primo grado - teoria ed esercizi
Alla scoperta delle equazioni di primo grado - teoria ed esercizi
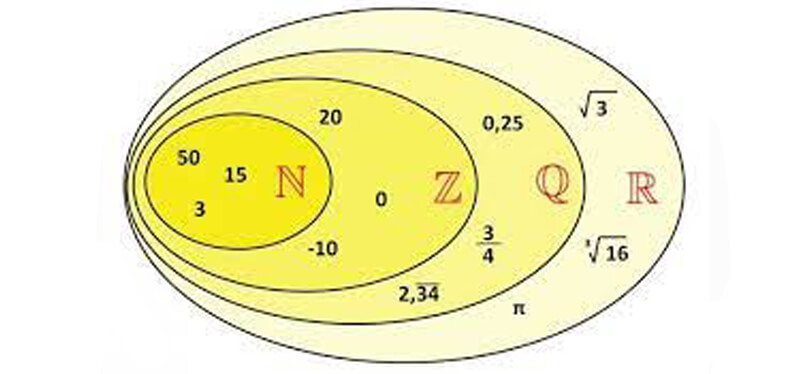 Numeri irrazionali - dalla teoria agli esercizi pratici
Numeri irrazionali - dalla teoria agli esercizi pratici