Identità Trigonometriche: Guida Completa con Esercizi Risolti
1) Introduzione
2) Cosa Sono le Identità Trigonometriche?
3) Identità Fondamentali
4) Identità di Somma e Differenza
5) Identità di Duplicazione e Bisezione
6) Identità di Prodotto-Somma
7) Esercizio Avanzato - Dimostrazione con Identità
7) Applicazioni delle Identità Trigonometriche
8) Conclusioni
Introduzione
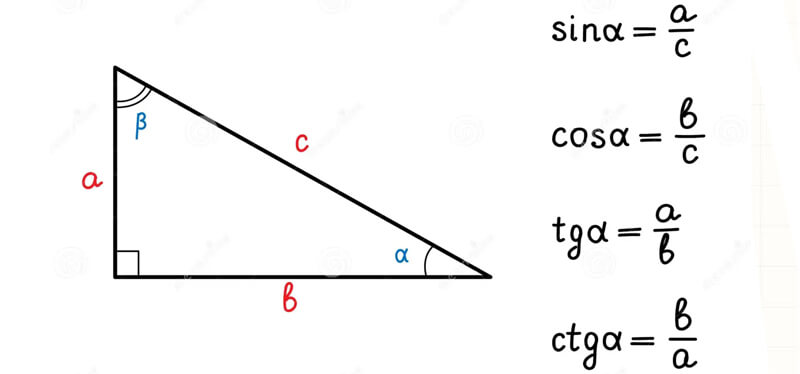
Le identità trigonometriche sono relazioni fondamentali che collegano seno, coseno, tangente e altre funzioni trigonometriche. Sono strumenti potenti in algebra, fisica e ingegneria e semplificano calcoli e risoluzione di equazioni.
Questa guida ti porterà dalle basi fino alle identità più avanzate, con spiegazioni chiare e esercizi risolti per ogni livello.
Cosa Sono le Identità Trigonometriche?
Le identità trigonometriche sono uguaglianze vere per ogni valore di x nel dominio delle funzioni coinvolte. Servono per semplificare espressioni, risolvere equazioni e dimostrare teoremi.
Le principali categorie sono:
✔ Identità fondamentali
✔ Identità di duplicazione e bisezione
✔ Identità di somma e differenza
✔ Identità di prodotto e somma
Identità Fondamentali
Le tre identità fondamentali della trigonometria sono:
Identità Pitagoriche
sin2(x) + cos2(x) = 1
1 + tan2(x) = 1/cos2(x)
1 + cot2(x) = 1/sin2(x)
Queste identità derivano direttamente dal teorema di Pitagora applicato al cerchio goniometrico.
Esercizio 1 - Verifica di un'Identità
Dimostra che:
sin2(x)/cos2(x) + 1 = 1/cos2(x)
Soluzione:
Usiamo l'identità pitagorica sin2(x) + cos2(x) = 1, dividiamo entrambi i membri per cos2(x):
sin2(x)/cos2(x) + cos2(x)/cos2(x) = 1/cos2(x)
tan2(x) + 1 = 1/cos2(x)
Quindi l'identità è verificata! ✅
Identità di Somma e Differenza
Queste identità permettono di calcolare il seno e il coseno di somme o differenze di angoli:
sin(A ± B) = sinAcosB ± cosAsinB
cos(A ± B) = cosAcosB ± sinAsinB
tan(A ± B) = (tanA ± tanB) / (1 ± tanAtanB)
Esercizio 2 - Calcolo di sin75°
Usiamo l'identità della somma con 75° = 45° + 30°:
sin(75°) = sin(45° + 30°) = sin45°cos30° + cos45°sin30°
Sostituiamo i valori noti:
= √2/2 · √3/2 + √2/2 · 1/2
= √6/4 + √2/4 = (√6 + √2) / 4
Identità di Duplicazione e Bisezione
Le identità di duplicazione si usano per esprimere funzioni trigonometriche di 2x in termini di x:
sin(2x) = 2sinxcosx
cos(2x) = cos2x − sin2x = 2cos2x − 1 = 1 − 2sin2x
tan(2x) = 2tanx / (1 − tan2x)
Esercizio 3 - Calcolo di cos2x con sinx = 3/5
Sappiamo che:
cos(2x) = 1 − 2sin2x
Calcoliamo sin2x:
sin2x = (3/5)2 = 9/25
Ora:
cos(2x) = 1 − 2 · 9/25 = 1 − 18/25 = 7/25
Identità di Prodotto-Somma
Queste identità trasformano un prodotto in una somma, molto utili in analisi e fisica:
sinAsinB = 1/2[cos(A − B) − cos(A + B)]
cosAcosB = 1/2[cos(A − B) + cos(A + B)]
sinAcosB = 1/2[sin(A + B) + sin(A - B)]
Esercizio Avanzato - Dimostrazione con Identità
Dimostra che:
(1 − cos2x) / sin2x = tanx
Soluzione:
Usiamo l'identità cos2x = 1 − 2sin2x:
(1 - (1 − 2sin2x)) / sin2x = 2sin2x / 2sinxcosx
Semplificando:
sinx / cosx = tanx
Identità verificata! ✅
Applicazioni delle Identità Trigonometriche
📌 Fisica: analisi delle onde, circuiti elettrici, meccanica rotazionale
📌 Ingegneria: elaborazione del segnale, calcoli strutturali
📌 Matematica avanzata: numeri complessi, Fourier, equazioni differenziali
Conclusioni
Ora conosci le identità trigonometriche principali e sai come applicarle. Se vuoi esercitarti ancora, prova a dimostrare altre identità o risolvere equazioni trigonometriche più complesse!
Fonti: libri scolastici superiori

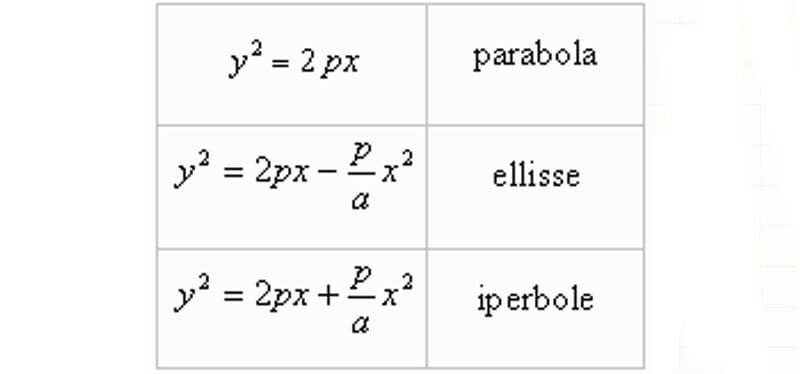 Equazione della parabola ellisse e iperbole - guida completa con esercizi risolti
Equazione della parabola ellisse e iperbole - guida completa con esercizi risolti
 Equazione della circonferenza - guida completa con esercizi risolti
Equazione della circonferenza - guida completa con esercizi risolti
 Logaritmi ed esponenziali - guida completa con esercizi risolti
Logaritmi ed esponenziali - guida completa con esercizi risolti
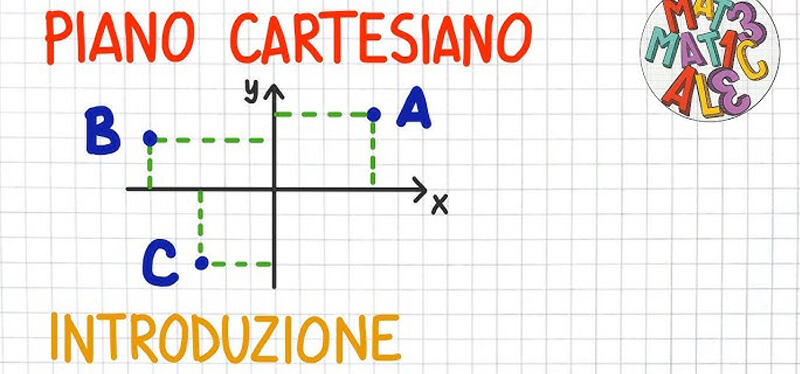 Il piano cartesiano - guida completa con esercizi risolti
Il piano cartesiano - guida completa con esercizi risolti
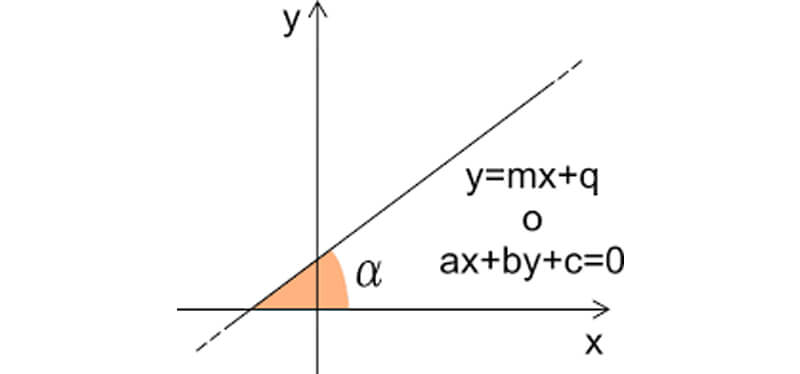 La retta - equazione e coefficiente angolare - guida completa con esercizi risolti
La retta - equazione e coefficiente angolare - guida completa con esercizi risolti
 Teorema dei seni e teorema del coseno - guida completa con esercizi risolti
Teorema dei seni e teorema del coseno - guida completa con esercizi risolti
 Seno coseno e tangente - guida completa con esercizi risolti
Seno coseno e tangente - guida completa con esercizi risolti
 Radicali e numeri complessi - guida completa con esercizi risolti
Radicali e numeri complessi - guida completa con esercizi risolti
 Guida completa alle disequazioni di secondo grado - teoria esercizi e approfondimenti
Guida completa alle disequazioni di secondo grado - teoria esercizi e approfondimenti
 Guida completa alle equazioni di secondo grado - teoria esercizi e aprofondimenti
Guida completa alle equazioni di secondo grado - teoria esercizi e aprofondimenti
 Guida completa al calcolo delle probabilita - teoria esercizi e approfondimenti
Guida completa al calcolo delle probabilita - teoria esercizi e approfondimenti
 Media moda e mediana - la statistica per tutti
Media moda e mediana - la statistica per tutti
 Le funzioni in matematica - guida completa con esercizi per tutti i livelli
Le funzioni in matematica - guida completa con esercizi per tutti i livelli
 Isometrie e similitudini - teoria esercizi e applicazioni
Isometrie e similitudini - teoria esercizi e applicazioni
 Introduzione alla geometria euclidea - teoria esercizi e approfondimenti
Introduzione alla geometria euclidea - teoria esercizi e approfondimenti
 Guida ai prodotti notevoli - teoria esercizi e applicazioni
Guida ai prodotti notevoli - teoria esercizi e applicazioni
 Alla scoperta delle disequazioni di primo grado - teoria ed esercizi
Alla scoperta delle disequazioni di primo grado - teoria ed esercizi
 Alla scoperta delle equazioni di primo grado - teoria ed esercizi
Alla scoperta delle equazioni di primo grado - teoria ed esercizi
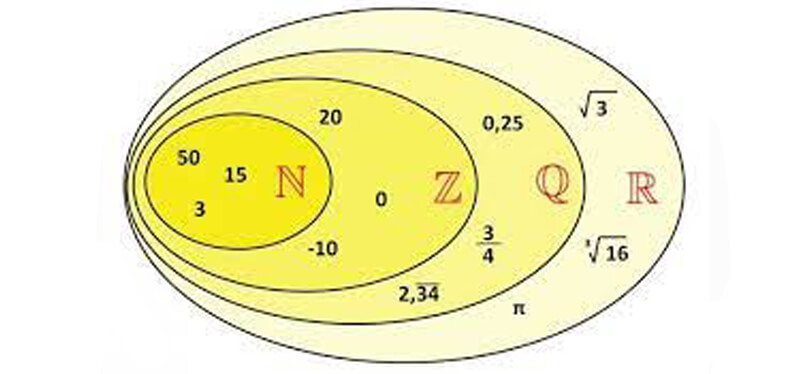 Numeri irrazionali - dalla teoria agli esercizi pratici
Numeri irrazionali - dalla teoria agli esercizi pratici