Logaritmi ed Esponenziali: Guida Completa con Esercizi Risolti

1) Introduzione
2) Funzioni Esponenziali: Definizione e Proprietà
3) Logaritmi: Definizione e Proprietà
4) Esercizi Risolti per Ogni Livello
5) Applicazioni Avanzate dei Logaritmi e degli Esponenziali
6) Conclusioni
Introduzione
I logaritmi e le funzioni esponenziali sono strumenti fondamentali in matematica, con applicazioni in fisica, economia, informatica e biologia.
Questa guida copre tutto: dalla definizione alle proprietà avanzate, con esercizi per ogni livello di difficoltà.
Funzioni Esponenziali: Definizione e Proprietà
Una funzione esponenziale ha la forma: f(x) = ax
dove:
a è la base (un numero positivo, a > 0 e a ≠ 1),
x è l'esponente.
Esempi di funzioni esponenziali:
2x, 3x, ex
Dove e ~ 2.718 è la base dei logaritmi naturali, chiamata numero di Eulero.
Proprietà delle funzioni esponenziali
Moltiplicazione di potenze con la stessa base:
am · an = am+n
Divisione di potenze con la stessa base:
am / an = am-n
Potenza di una potenza:
(am)n = am·n
Esponente negativo:
a-n = 1 / an
Esponente frazionario:
am/n = n√am
Logaritmi: Definizione e Proprietà
Il logaritmo è l'operazione inversa dell'esponenziale. Il logaritmo in base a di un numero b è l'esponente a cui bisogna elevare a per ottenere b: logab = x se e solo se ax = b
Esempi:
log28 = 3 perché 23 = 8
log327 = 3 perché 33 = 27
Tipi di logaritmi
Logaritmo decimale: logx(base 10)
Logaritmo naturale: lnx (base e)
Proprietà fondamentali dei logaritmi
Logaritmo di un prodotto:
loga(xy) = logax + logay
Logaritmo di un quoziente:
loga(x / y) = logax - logay
Logaritmo di una potenza:
log2(xn) = nlogax
Cambiamento di base:
logab = logcb / logca
Esercizi Risolti per Ogni Livello
Esercizio 1 - Base: Calcolo di Esponenziali
Calcola: 34 e 5-2
Soluzione:
34 = 3 x 3 x 3 x 3 = 81
5-2 = 1 / 52 = 1 / 25
Esercizio 2 - Base: Calcolo di Logaritmi
Calcola log216 e log5125
Soluzione:
log216 = 4 (perché 24 = 16)
log2125 = 3 (perché 53 = 125)
Esercizio 3 - Intermedio: Semplificazione di Logaritmi
Semplifica l'espressione: log3(27·9)
Soluzione:
Usiamo la proprietà del prodotto:
log3(27·9) = log327 + log39
Poiché 27 = 33 e 9 = 32, otteniamo:
log327 = 3, log39 = 2
log3(27·9) = 3 + 2 = 5
Esercizio 4 - Avanzato: Risoluzione di un'Equazione Logaritmica
Risolvi l'equazione: log2(x - 1) + log2(x + 3) = 3
Soluzione:
Usiamo la proprietà del prodotto:
log2[(x - 1)(x + 3)] = 3
Convertiamo in forma esponenziale:
(x - 1)(x + 3) = 23
x2 + 3x - x - 3 = 8
x2 + 2x - 11 = 0
Risolvendo con la formula del delta:
Δ = 22 - 4(1)(-11) = 4 + 44 = 48
x = (-2 ± √48) / 2 = (-2 ± 4√3) / 2 = -1 ± 2√3
Essendo x − 1 > 0, scegliamo x = −1 + 2√3
Applicazioni Avanzate dei Logaritmi e degli Esponenziali
✅ Crescita ed Estinzione: modelli di crescita delle popolazioni e decadimento radioattivo
✅ Economia e Finanza: interesse composto, crescita esponenziale dei capitali
✅ Informatica: complessità algoritmica (ad es. O(logn)
✅ Fisica e Ingegneria: equazioni differenziali, onde, vibrazioni
Conclusioni
Ora hai una panoramica completa su logaritmi ed esponenziali, con esercizi per ogni livello.
Se vuoi migliorare, prova a risolvere esercizi più difficili e applica questi concetti ai problemi reali!
Fonti: libri scolastici superiori

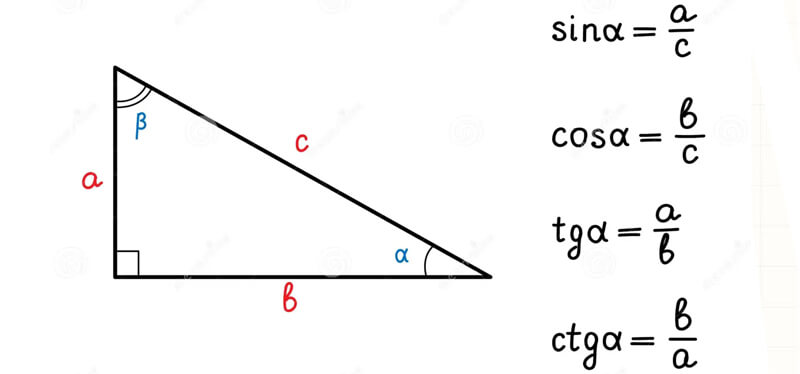 Identita trigonometriche - guida completa con esercizi risolti
Identita trigonometriche - guida completa con esercizi risolti
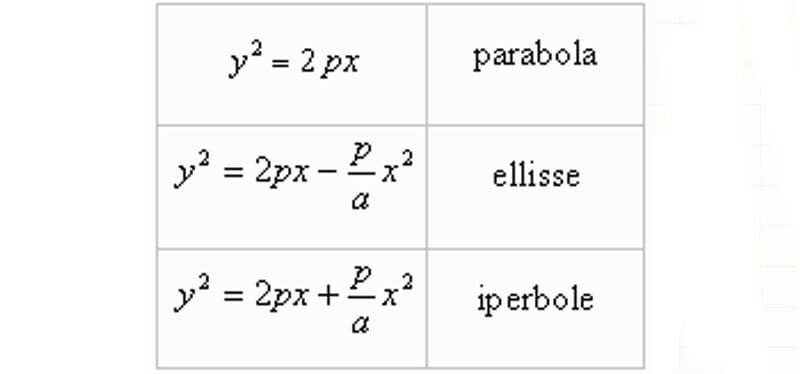 Equazione della parabola ellisse e iperbole - guida completa con esercizi risolti
Equazione della parabola ellisse e iperbole - guida completa con esercizi risolti
 Equazione della circonferenza - guida completa con esercizi risolti
Equazione della circonferenza - guida completa con esercizi risolti
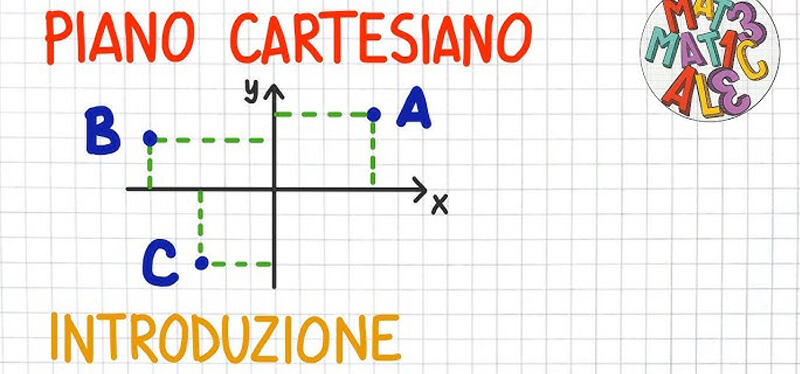 Il piano cartesiano - guida completa con esercizi risolti
Il piano cartesiano - guida completa con esercizi risolti
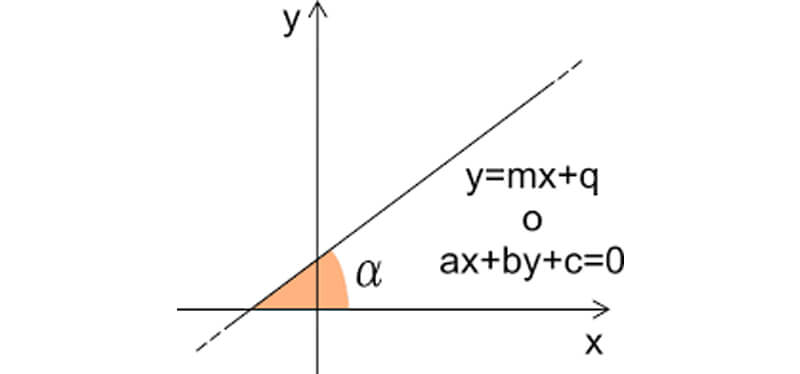 La retta - equazione e coefficiente angolare - guida completa con esercizi risolti
La retta - equazione e coefficiente angolare - guida completa con esercizi risolti
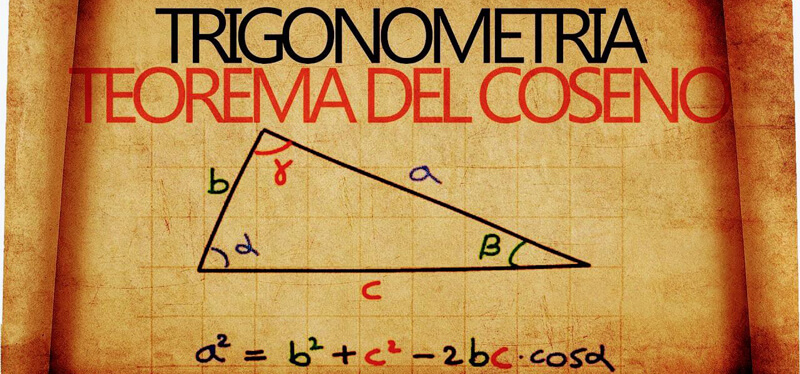 Teorema dei seni e teorema del coseno - guida completa con esercizi risolti
Teorema dei seni e teorema del coseno - guida completa con esercizi risolti
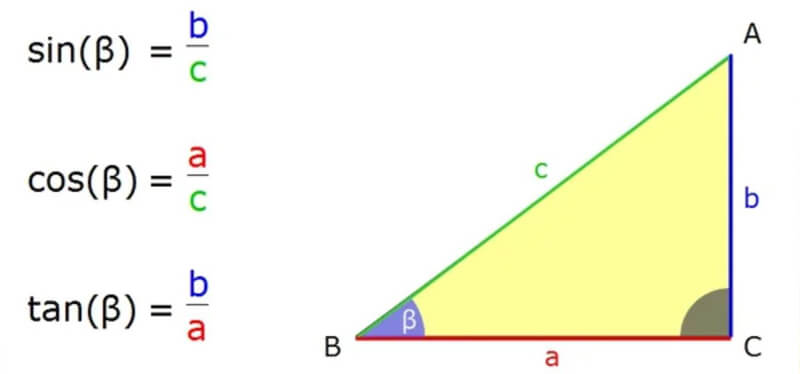 Seno coseno e tangente - guida completa con esercizi risolti
Seno coseno e tangente - guida completa con esercizi risolti
 Radicali e numeri complessi - guida completa con esercizi risolti
Radicali e numeri complessi - guida completa con esercizi risolti
 Guida completa alle disequazioni di secondo grado - teoria esercizi e approfondimenti
Guida completa alle disequazioni di secondo grado - teoria esercizi e approfondimenti
 Guida completa alle equazioni di secondo grado - teoria esercizi e aprofondimenti
Guida completa alle equazioni di secondo grado - teoria esercizi e aprofondimenti
 Guida completa al calcolo delle probabilita - teoria esercizi e approfondimenti
Guida completa al calcolo delle probabilita - teoria esercizi e approfondimenti
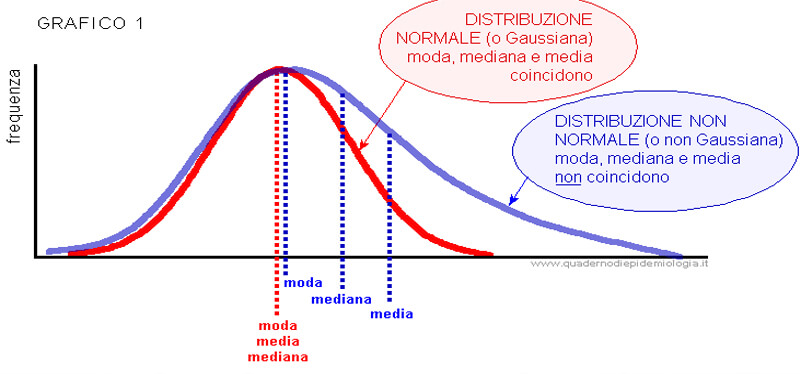 Media moda e mediana - la statistica per tutti
Media moda e mediana - la statistica per tutti
 Le funzioni in matematica - guida completa con esercizi per tutti i livelli
Le funzioni in matematica - guida completa con esercizi per tutti i livelli
 Isometrie e similitudini - teoria esercizi e applicazioni
Isometrie e similitudini - teoria esercizi e applicazioni
 Introduzione alla geometria euclidea - teoria esercizi e approfondimenti
Introduzione alla geometria euclidea - teoria esercizi e approfondimenti
 Guida ai prodotti notevoli - teoria esercizi e applicazioni
Guida ai prodotti notevoli - teoria esercizi e applicazioni
 Alla scoperta delle disequazioni di primo grado - teoria ed esercizi
Alla scoperta delle disequazioni di primo grado - teoria ed esercizi
 Alla scoperta delle equazioni di primo grado - teoria ed esercizi
Alla scoperta delle equazioni di primo grado - teoria ed esercizi
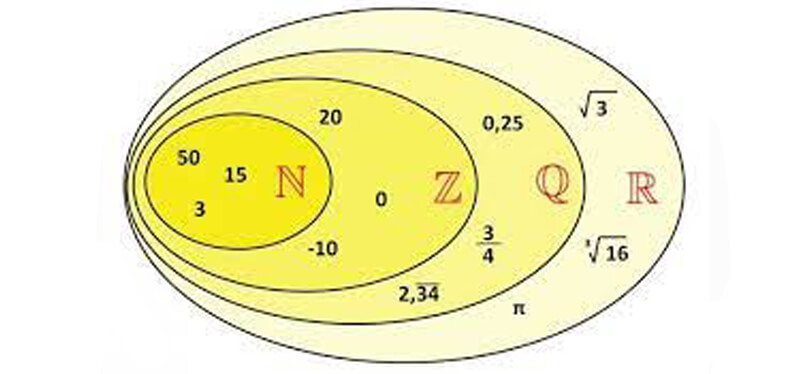 Numeri irrazionali - dalla teoria agli esercizi pratici
Numeri irrazionali - dalla teoria agli esercizi pratici