Seno, Coseno e Tangente: Guida Completa con Esercizi Risolti
1) Introduzione
2) Definizione di Seno, Coseno e Tangente
3) Il Cerchio Goniometrico e le Funzioni Trigonometriche
4) Identità Trigonometriche Fondamentali
5) Esercizi Pratici
6) Applicazioni delle Funzioni Trigonometriche
7) Conclusioni
Introduzione
Il seno, il coseno e la tangente sono concetti fondamentali della trigonometria, essenziali per risolvere problemi di geometria, fisica e ingegneria.
In questa guida partiremo dalle basi e arriveremo a concetti avanzati, con esercizi risolti per tutti i livelli.
Definizione di Seno, Coseno e Tangente
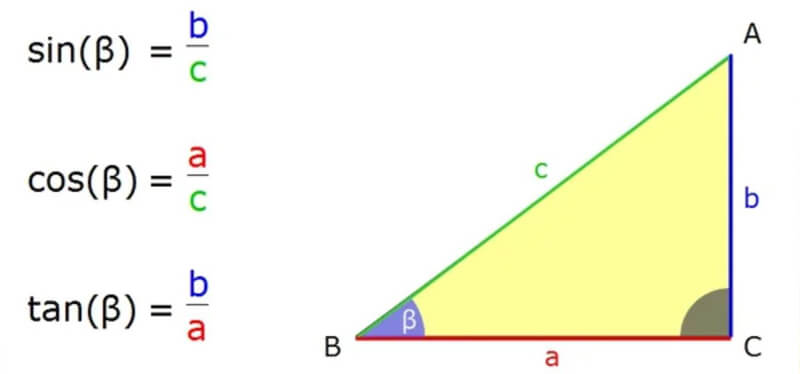
Il seno, il coseno e la tangente sono funzioni trigonometriche che si basano sui triangoli rettangoli. Supponiamo di avere un triangolo rettangolo con:
- Ipotenusa = il lato più lungo, opposto all'angolo retto
- Cateto opposto = il lato di fronte all’angolo considerato
- Cateto adiacente = il lato accanto all’angolo considerato
Le tre funzioni principali si definiscono come:
sin(θ) = cateto opposto / ipotenusa
cos(θ) = cateto adiacente / ipotenusa
tan(θ) = cateto opposto / cateto adiacente
Esempio Pratico
Immaginiamo un triangolo rettangolo con:
Ipotenusa = 10
Cateto opposto = 6
Cateto adiacente = 8
Calcoliamo le funzioni trigonometriche:
sin(θ) = 6 / 10 = 0.6
cos(θ) = 8 / 10 = 0.8
tan(θ) = 6 / 8 = 0.75
Il Cerchio Goniometrico e le Funzioni Trigonometriche
Per generalizzare seno, coseno e tangente a tutti gli angoli, utilizziamo il cerchio goniometrico (raggio = 1).
Il seno di un angolo corrisponde alla coordinata y del punto sulla circonferenza.
Il coseno corrisponde alla coordinata x.
La tangente è il rapporto y / x.
Valori Notevoli:
sin 0° = 0
cos 0° = 1
tan 0° = 0
sin 30° = 1 / 2
cos 30° = √3 / 2
tan 30° = √3 / 3
sin 45° = √2 / 2
cos 45° = √2 / 2
tan 45° = 1
sin 60° = √3 / 2
cos 60° = 1 / 2
tan 60° = √3
sin 90° = 1
cos 90° = 0
tan 90° = non definita
Identità Trigonometriche Fondamentali
Le identità trigonometriche permettono di semplificare calcoli e risolvere equazioni trigonometriche.
Identità di base
sin2(θ) + cos2(θ) = 1
1 + tan2(θ) = 1 / cos2(θ)
sin(2θ) = 2sin(θ)cos(θ)
cos(2θ) = cos2(θ) − sin2(θ)
Esercizi Pratici
Esercizio 1: Triangolo Rettangolo (Base)
Problema:
Un triangolo rettangolo ha un'ipotenusa di 13 cm e un cateto di 5 cm. Calcola seno, coseno e tangente dell'angolo opposto al cateto noto.
Svolgimento:
Troviamo l'altro cateto con il teorema di Pitagora:
c2 = 132 − 52 = 169 − 25 = 144 => c = √144 = 12
Ora calcoliamo:
sin(θ) = 5 / 13
cos(θ) = 12 / 13
tan(θ) = 5 / 12
Esercizio 2: Equazione Trigonometrica (Intermedio)
Problema:
Risolvi l’equazione: 2sin(x) - 1 = 0 con 0° ≤ x ≤ 360°
Svolgimento:
sin(x) = 1 / 2
Dai valori notevoli:
x = 30° e x = 150°
Risultato:
x = 30°, 150°
Esercizio 3: Formula di De Moivre (Avanzato)
Problema:
Calcola (cos 45° + isin 45°)4
Svolgimento:
Usiamo la formula di De Moivre:
(cosθ + isinθ)n = cos(nθ) + isin(nθ)
(cos 45° + isin 45°)4 = cos(180°) + isin(180°) = −1 +i0 = −1
Applicazioni delle Funzioni Trigonometriche
Le funzioni trigonometriche trovano applicazione in:
✅ Fisica: oscillazioni armoniche, circuiti elettrici, onde sonore
✅ Ingegneria: calcoli strutturali, misurazioni angolari
✅ Matematica avanzata: numeri complessi, analisi di Fourier
Conclusioni
Ora hai una panoramica completa sul seno, coseno e tangente, dai concetti base alle applicazioni avanzate.
Se vuoi approfondire, prova a risolvere nuovi esercizi e sperimenta la trigonometria nel mondo reale!
Fonti: libri scolastici superiori

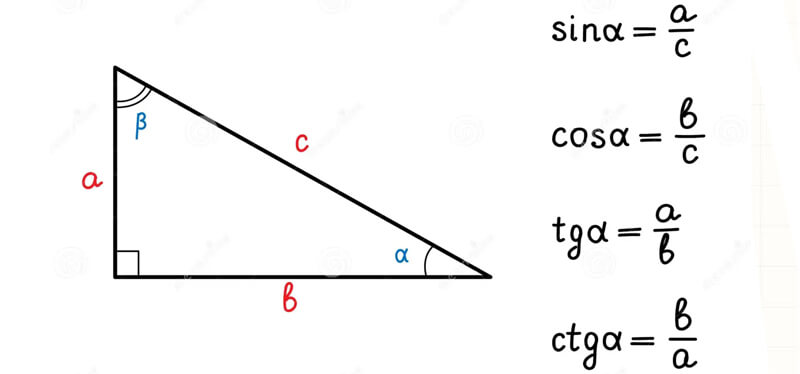 Identita trigonometriche - guida completa con esercizi risolti
Identita trigonometriche - guida completa con esercizi risolti
 Equazione della parabola ellisse e iperbole - guida completa con esercizi risolti
Equazione della parabola ellisse e iperbole - guida completa con esercizi risolti
 Equazione della circonferenza - guida completa con esercizi risolti
Equazione della circonferenza - guida completa con esercizi risolti
 Logaritmi ed esponenziali - guida completa con esercizi risolti
Logaritmi ed esponenziali - guida completa con esercizi risolti
 Il piano cartesiano - guida completa con esercizi risolti
Il piano cartesiano - guida completa con esercizi risolti
 La retta - equazione e coefficiente angolare - guida completa con esercizi risolti
La retta - equazione e coefficiente angolare - guida completa con esercizi risolti
 Teorema dei seni e teorema del coseno - guida completa con esercizi risolti
Teorema dei seni e teorema del coseno - guida completa con esercizi risolti
 Radicali e numeri complessi - guida completa con esercizi risolti
Radicali e numeri complessi - guida completa con esercizi risolti
 Guida completa alle disequazioni di secondo grado - teoria esercizi e approfondimenti
Guida completa alle disequazioni di secondo grado - teoria esercizi e approfondimenti
 Guida completa alle equazioni di secondo grado - teoria esercizi e aprofondimenti
Guida completa alle equazioni di secondo grado - teoria esercizi e aprofondimenti
 Guida completa al calcolo delle probabilita - teoria esercizi e approfondimenti
Guida completa al calcolo delle probabilita - teoria esercizi e approfondimenti
 Media moda e mediana - la statistica per tutti
Media moda e mediana - la statistica per tutti
 Le funzioni in matematica - guida completa con esercizi per tutti i livelli
Le funzioni in matematica - guida completa con esercizi per tutti i livelli
 Isometrie e similitudini - teoria esercizi e applicazioni
Isometrie e similitudini - teoria esercizi e applicazioni
 Introduzione alla geometria euclidea - teoria esercizi e approfondimenti
Introduzione alla geometria euclidea - teoria esercizi e approfondimenti
 Guida ai prodotti notevoli - teoria esercizi e applicazioni
Guida ai prodotti notevoli - teoria esercizi e applicazioni
 Alla scoperta delle disequazioni di primo grado - teoria ed esercizi
Alla scoperta delle disequazioni di primo grado - teoria ed esercizi
 Alla scoperta delle equazioni di primo grado - teoria ed esercizi
Alla scoperta delle equazioni di primo grado - teoria ed esercizi
 Numeri irrazionali - dalla teoria agli esercizi pratici
Numeri irrazionali - dalla teoria agli esercizi pratici