Il Piano Cartesiano: Guida Completa con Esercizi Risolti
1) Introduzione
2) Cos'è il Piano Cartesiano?
3) Distanza tra Due Punti
4) Il Punto Medio di un Segmento
5) Equazione della Retta
6) Esercizi Pratici
7) Applicazioni
8) Conclusioni
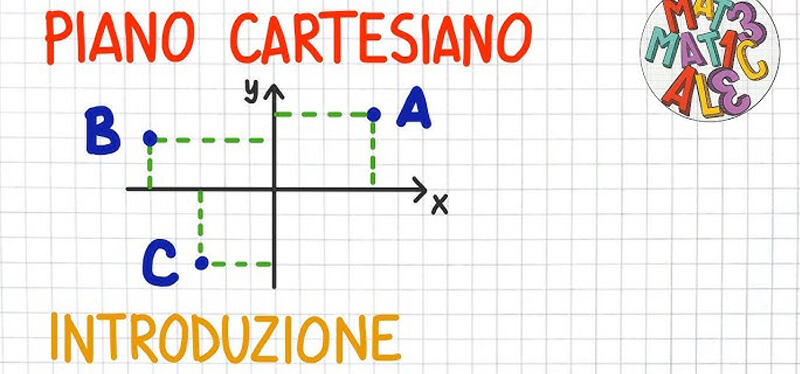
Introduzione
Il Piano Cartesiano è uno strumento essenziale in matematica, utilizzato per rappresentare punti, funzioni e figure geometriche.
Questa guida ti accompagnerà dalle basi alle applicazioni avanzate, con esercizi risolti per ogni livello.
Cos'è il Piano Cartesiano?
Il Piano Cartesiano è un sistema di riferimento bidimensionale, introdotto da René Descartes (Cartesio), formato da due rette perpendicolari:
Asse X (ascisse) -> orizzontale
Asse Y (ordinate) -> verticale
Il punto di intersezione è detto origine O(0,0).
Suddivisione del Piano
Il piano è diviso in quattro quadranti:
I quadrante:
x > 0, y > 0
II quadrante:
x < 0, y > 0
III quadrante:
x < 0, y < 0
IV quadrante:
x > 0, y < 0
Esempio:
Posizionamento di un Punto
Il punto A(3, −2):
✅ La coordinata x = 3 significa che ci spostiamo a destra di 3 unità.
✅ La coordinata y = −2 significa che scendiamo di 2 unità.
📍 Il punto si trova nel IV quadrante.
Distanza tra Due Punti
La distanza tra due punti A(x1, y1) e B(x2, y2) è calcolata con la formula della distanza:
d(A, B) = √(x2 − x1)2 + (y2 − y1)2
Esercizio 1 - Calcolo della Distanza
Trova la distanza tra i punti A(1, 2) e B(4, 6).
Soluzione:
d = √(4 − 1)2 + (6 − 2)2 = √32 + 42 = √9 + 16 = √25 = 5
Il Punto Medio di un Segmento
La formula del punto medio tra A(x1, y1) e B(x2, y2) è:
M( (x1 + x2) / 2, y1 + y2) / 2 )
Esercizio 2 - Trova il Punto Medio
Trova il punto medio del segmento con estremi A(2, 3) e (8, 7).
Soluzione:
M( (2 + 8) / 2, (3 + 7) / 2) = M(5, 5)
Equazione della Retta
L’equazione generale di una retta è: y = mx + q
Dove:
m è il coefficiente angolare, che indica l'inclinazione della retta.
q è l'intercetta con l'asse y (valore di y quando x = 0).
Formula del Coefficiente Angolare
Se una retta passa per due punti A(x1, y1) e B(x2, y2), la pendenza è data da: m = (y2 − y1) / (x2 − x1)
Esercizio 3 - Determinare l'Equazione di una Retta
Trova l'equazione della retta passante per i punti A(1, 2) e B(4, 5).
Soluzione:
Troviamo la pendenza:
m = (5 − 2) / (4 − 1) = 3 / 3 = 1
Ora usiamo la formula y = mx + q, sostituendo A(1, 2):
2 = 1(1) + q => q = 1
Equazione della retta: y = x + 1
Geometria Analitica Avanzata
Rette Parallele e Perpendicolari
Rette parallele: hanno lo stesso coefficiente angolare m1 = m2
Rette perpendicolari: i coefficienti angolari sono reciproci e opposti: m1 · m2 = -1
Esercizio 4 - Verifica se Due Rette sono Perpendicolari
Le rette y = 2x + 3 e y = −1/2x + 5 sono perpendicolari?
Soluzione:
Moltiplichiamo i coefficienti angolari: 2 x (−1/2) = −1
✅ Le rette sono perpendicolari.
Applicazioni
✅ Fisica: Moto dei proiettili, traiettorie, calcolo della velocità.
✅ Ingegneria: Strutture, coordinate in costruzioni.
✅ Grafica e Computer Science: Rendering 3D, collisioni tra oggetti.
Conclusioni
Ora hai una comprensione completa del Piano Cartesiano, dai concetti base alle applicazioni avanzate! Prova altri esercizi e scopri come usarlo in problemi più complessi.
Fonti: libri scolastici superiori

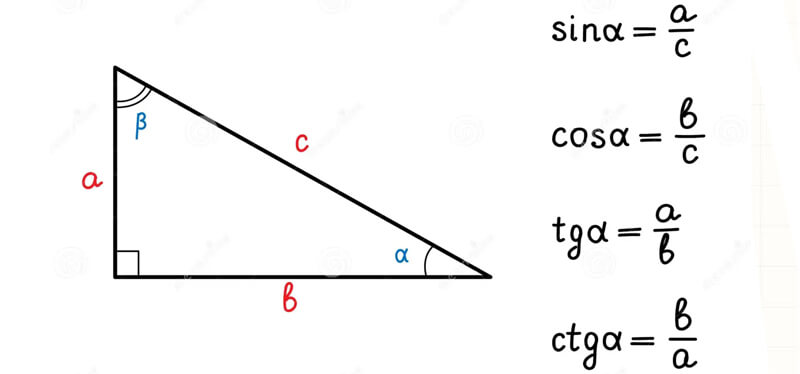 Identita trigonometriche - guida completa con esercizi risolti
Identita trigonometriche - guida completa con esercizi risolti
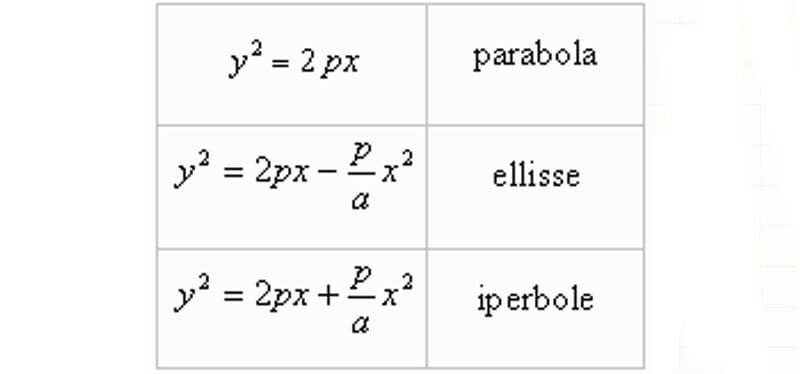 Equazione della parabola ellisse e iperbole - guida completa con esercizi risolti
Equazione della parabola ellisse e iperbole - guida completa con esercizi risolti
 Equazione della circonferenza - guida completa con esercizi risolti
Equazione della circonferenza - guida completa con esercizi risolti
 Logaritmi ed esponenziali - guida completa con esercizi risolti
Logaritmi ed esponenziali - guida completa con esercizi risolti
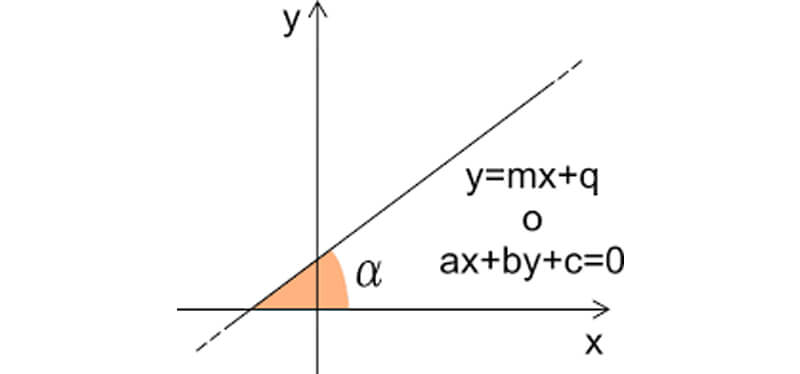 La retta - equazione e coefficiente angolare - guida completa con esercizi risolti
La retta - equazione e coefficiente angolare - guida completa con esercizi risolti
 Teorema dei seni e teorema del coseno - guida completa con esercizi risolti
Teorema dei seni e teorema del coseno - guida completa con esercizi risolti
 Seno coseno e tangente - guida completa con esercizi risolti
Seno coseno e tangente - guida completa con esercizi risolti
 Radicali e numeri complessi - guida completa con esercizi risolti
Radicali e numeri complessi - guida completa con esercizi risolti
 Guida completa alle disequazioni di secondo grado - teoria esercizi e approfondimenti
Guida completa alle disequazioni di secondo grado - teoria esercizi e approfondimenti
 Guida completa alle equazioni di secondo grado - teoria esercizi e aprofondimenti
Guida completa alle equazioni di secondo grado - teoria esercizi e aprofondimenti
 Guida completa al calcolo delle probabilita - teoria esercizi e approfondimenti
Guida completa al calcolo delle probabilita - teoria esercizi e approfondimenti
 Media moda e mediana - la statistica per tutti
Media moda e mediana - la statistica per tutti
 Le funzioni in matematica - guida completa con esercizi per tutti i livelli
Le funzioni in matematica - guida completa con esercizi per tutti i livelli
 Isometrie e similitudini - teoria esercizi e applicazioni
Isometrie e similitudini - teoria esercizi e applicazioni
 Introduzione alla geometria euclidea - teoria esercizi e approfondimenti
Introduzione alla geometria euclidea - teoria esercizi e approfondimenti
 Guida ai prodotti notevoli - teoria esercizi e applicazioni
Guida ai prodotti notevoli - teoria esercizi e applicazioni
 Alla scoperta delle disequazioni di primo grado - teoria ed esercizi
Alla scoperta delle disequazioni di primo grado - teoria ed esercizi
 Alla scoperta delle equazioni di primo grado - teoria ed esercizi
Alla scoperta delle equazioni di primo grado - teoria ed esercizi
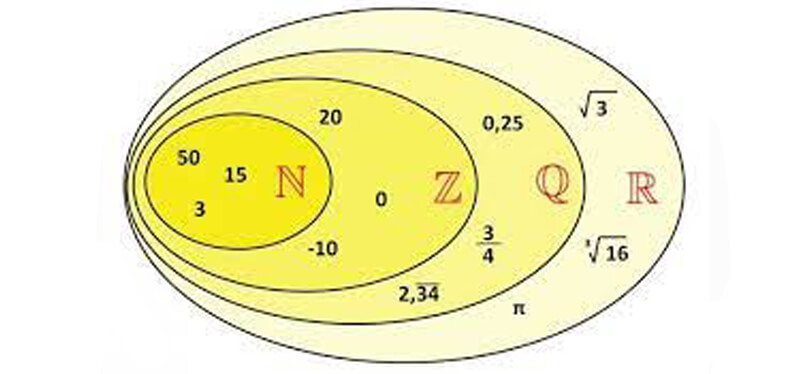 Numeri irrazionali - dalla teoria agli esercizi pratici
Numeri irrazionali - dalla teoria agli esercizi pratici