Radicali e Numeri Complessi: Guida Completa con Esercizi Risolti

1) Introduzione
2) I Radicali: Definizione e Proprietà Fondamentali
3) Numeri Complessi: Introduzione e Proprietà
4) Forma Polare e Esponenziale dei Numeri Complessi
5) Conclusioni
Introduzione
I radicali e i numeri complessi sono concetti fondamentali in matematica, con applicazioni che spaziano dall'algebra all'analisi, fino alla fisica e all'ingegneria.
In questa guida, partiremo dalle basi per arrivare a concetti avanzati, arricchendo il tutto con esercizi risolti per ogni livello di difficoltà.
I Radicali: Definizione e Proprietà Fondamentali
Un radicale è un'espressione del tipo: n√a
dove:
- n è l’indice del radicale,
- a è il radicando.
Se n = 2, il radicale è una radice quadrata, mentre se n = 3, è una radice cubica.
Proprietà fondamentali dei radicali
1) Moltiplicazione e divisione sotto radice:
n√a · n√b = n√a · b
(n√a) / (n√b) = n√a / b
2) Elevamento a potenza e semplificazione:
(n√a)n = a
n√am = am / n
3) Razionalizzazione (eliminazione del radicale al denominatore):
Se il denominatore contiene una radice quadrata, moltiplichiamo numeratore e denominatore per la radice stessa.
Se il denominatore è un binomio con radice, usiamo il coniugato.
Esercizio 1 - Semplificazione di Radicali
Semplifica l'espressione: 5 / √3
Soluzione:
Moltiplichiamo numeratore e denominatore per √3:
(5 / √3) x (√3 / √3) = 5√3 / 3
Numeri Complessi: Introduzione e Proprietà
I numeri complessi si basano sull'unità immaginaria i, definita come: i2 = −1
Un numero complesso ha la forma: z = a + bi
dove a è la parte reale e b è la parte immaginaria.
Operazioni con i numeri complessi
1) Somma e differenza
(a + bi) + (c + di) = (a + c) + (b + d)i
2) Moltiplicazione
(a + bi) · (c + di) = (ac − bd) + (ad + bc)i
3) Divisione
(a + bi) / (c + di) = (a + bi)(c − di) / (c2 + d2)
4) Modulo e coniugato
|z| = √a2 + b2
z = a - bi
Esercizio 2 - Prodotto di Numeri Complessi
Calcola il prodotto: (3 + 2i) · (1 − 4i)
Soluzione:
(3 + 2i)(1 − 4i) = 3 −12i +2i −8i2
Poiché i2 = −1, otteniamo:
3 −12i +2i + 8 = 11 −10i
Forma Polare e Esponenziale dei Numeri Complessi
Un numero complesso può essere espresso anche in forma polare: z = r(cosθ + isinθ)
dove:
r = |z| = √a2 + b2 è il modulo,
θ = arg(z) = tan-1(b / a) è l’argomento.
In forma esponenziale:
z = reiθ
Grazie alla formula di De Moivre, possiamo elevare un numero complesso a una potenza in modo semplice: (zn = rneinθ)
Esercizio 3 - Elevamento a Potenza con De Moivre
Calcola (1 + i)4 in forma polare.
Soluzione:
Troviamo il modulo:
r = |1 + i| = √12 + 12 = √2
Troviamo l’argomento:
θ = tan−1(1 / 1) = π / 4
Usiamo De Moivre:
(1 + i) 4 = (√2)4ei4(π / 4) = 4eiπ = -4
Conclusioni
Abbiamo esplorato radicali e numeri complessi in dettaglio, dalle basi alle applicazioni avanzate.
Se vuoi approfondire ulteriormente, continua con esercizi più complessi e scopri come i numeri complessi vengono utilizzati in fisica e ingegneria!
Fonti: libri scolastici superiori

 Identita trigonometriche - guida completa con esercizi risolti
Identita trigonometriche - guida completa con esercizi risolti
 Equazione della parabola ellisse e iperbole - guida completa con esercizi risolti
Equazione della parabola ellisse e iperbole - guida completa con esercizi risolti
 Equazione della circonferenza - guida completa con esercizi risolti
Equazione della circonferenza - guida completa con esercizi risolti
 Logaritmi ed esponenziali - guida completa con esercizi risolti
Logaritmi ed esponenziali - guida completa con esercizi risolti
 Il piano cartesiano - guida completa con esercizi risolti
Il piano cartesiano - guida completa con esercizi risolti
 La retta - equazione e coefficiente angolare - guida completa con esercizi risolti
La retta - equazione e coefficiente angolare - guida completa con esercizi risolti
 Teorema dei seni e teorema del coseno - guida completa con esercizi risolti
Teorema dei seni e teorema del coseno - guida completa con esercizi risolti
 Seno coseno e tangente - guida completa con esercizi risolti
Seno coseno e tangente - guida completa con esercizi risolti
 Guida completa alle disequazioni di secondo grado - teoria esercizi e approfondimenti
Guida completa alle disequazioni di secondo grado - teoria esercizi e approfondimenti
 Guida completa alle equazioni di secondo grado - teoria esercizi e aprofondimenti
Guida completa alle equazioni di secondo grado - teoria esercizi e aprofondimenti
 Guida completa al calcolo delle probabilita - teoria esercizi e approfondimenti
Guida completa al calcolo delle probabilita - teoria esercizi e approfondimenti
 Media moda e mediana - la statistica per tutti
Media moda e mediana - la statistica per tutti
 Le funzioni in matematica - guida completa con esercizi per tutti i livelli
Le funzioni in matematica - guida completa con esercizi per tutti i livelli
 Isometrie e similitudini - teoria esercizi e applicazioni
Isometrie e similitudini - teoria esercizi e applicazioni
 Introduzione alla geometria euclidea - teoria esercizi e approfondimenti
Introduzione alla geometria euclidea - teoria esercizi e approfondimenti
 Guida ai prodotti notevoli - teoria esercizi e applicazioni
Guida ai prodotti notevoli - teoria esercizi e applicazioni
 Alla scoperta delle disequazioni di primo grado - teoria ed esercizi
Alla scoperta delle disequazioni di primo grado - teoria ed esercizi
 Alla scoperta delle equazioni di primo grado - teoria ed esercizi
Alla scoperta delle equazioni di primo grado - teoria ed esercizi
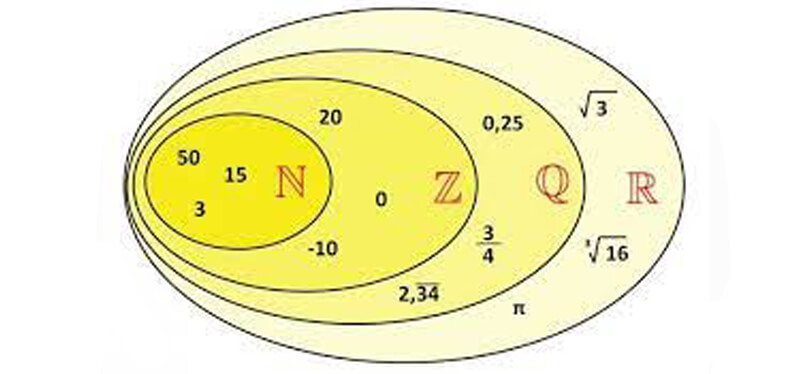 Numeri irrazionali - dalla teoria agli esercizi pratici
Numeri irrazionali - dalla teoria agli esercizi pratici