Media, Moda e Mediana: La Statistica per Tutti
1) Introduzione
2) Cosa Sono Media, Moda e Mediana?
3) La Media Aritmetica: La Più Conosciuta
4) La Moda: Il Valore Più Frequente
5) La Mediana: Il Valore Centrale
6) Esercizi Pratici: Dalle Basi agli Approfondimenti
7) Curiosità e Applicazioni
8) Conclusioni
Introduzione
La statistica è ovunque: dai voti scolastici alle previsioni meteo, dalle analisi di mercato alle ricerche scientifiche. Ma come possiamo sintetizzare un insieme di dati per ottenere informazioni utili?
Tre strumenti fondamentali per questo scopo sono media, moda e mediana.
Cosa Sono Media, Moda e Mediana?
Quando abbiamo un insieme di dati numerici, spesso vogliamo trovare un "valore rappresentativo". I tre principali indicatori di tendenza centrale sono:
Media aritmetica: il valore "medio" ottenuto sommando tutti i dati e dividendo per il numero totale di elementi.
Moda: il valore che compare più frequentemente nel dataset.
Mediana: il valore centrale quando i dati sono ordinati in ordine crescente.
Ognuna di queste misure ha applicazioni e utilizzi diversi. Vediamo nel dettaglio come calcolarle.
La Media Aritmetica: La Più Conosciuta
Definizione:
La media aritmetica si calcola sommando tutti i valori e dividendo il totale per il numero di elementi.
Formula:
Media = (x1 + x2 + ... + xn) / n dove x1, x2, ..., xn sono i dati e n è il numero totale di elementi.
Esempio:
Problema: Il professor Rossi ha dato questi voti ai suoi studenti: 7, 8, 6, 9, 8.
Qual è la media dei voti?
Soluzione:
Media = (7 + 8 + 6 + 9 + 8) / 5 = 38/5 = 7.6
Risultato: La media dei voti è 7.6.
Quando Usare la Media?
- Per ottenere una visione generale dei dati.
- Quando i valori sono distribuiti in modo uniforme.
- Utile in pagelle scolastiche, statistiche aziendali, scienze e finanza.
Limiti della media: Se un dato è molto più grande o più piccolo degli altri (outlier), può distorcere il risultato.
La Moda: Il Valore Più Frequente
Definizione:
La moda è il valore che compare più spesso in un insieme di dati.
Esempio:
Problema: Consideriamo il seguente set di dati: 2, 3, 3, 5, 7, 3, 8.
Qual è la moda?
Soluzione:
Il numero 3 compare più volte degli altri (tre volte).
Risultato: La moda è 3.
Casi particolari della moda:
Se tutti i valori compaiono lo stesso numero di volte, non esiste una moda.
Se due o più valori compaiono con la stessa frequenza massima, il dataset è bimodale o multimodale.
Quando usare la moda?
Utile nelle preferenze dei consumatori, nei sondaggi e nelle analisi di mercato.
Adatta per dati qualitativi (es. il colore più venduto di un'auto).
La Mediana: Il Valore Centrale
Definizione:
La mediana è il valore centrale di un insieme di dati ordinati.
Metodo di Calcolo:
1) Ordina i dati in ordine crescente.
2) Se il numero di dati è dispari, la mediana è il valore centrale.
3) Se il numero di dati è pari, la mediana è la media dei due valori centrali.
Esempio:
Problema 1 (numero dispari di elementi): Trova la mediana dei numeri: 5, 3, 8, 7, 2.
Soluzione:
1) Ordiniamo i numeri: 2, 3, 5, 7, 8
2) Il numero centrale è 5.
Risultato: La mediana è 5.
Problema 2 (numero pari di elementi):
Trova la mediana dei numeri: 12, 4, 9, 6.
Soluzione:
1) Ordiniamo i numeri: 4, 6, 9, 12
2) Ci sono due valori centrali: 6 e 9.
3) Facciamo la media
Mediana = (6 + 9) / 2 = 15/2 = 7.5
Risultato: La mediana è 7.5.
Quando Usare la Mediana?
Utile quando ci sono outlier, perché non è influenzata da valori estremi.
Applicata in analisi economiche (redditi mediani), prezzi immobiliari, distribuzione del reddito.
Esercizi Pratici: Dalle Basi agli Approfondimenti
Esercizio 1: Calcolo della Media
Problema:
Dati i numeri: 4, 7, 10, 5, 8, 6, calcola la media.
Svolgimento:
Media = (4 + 7 + 10 + 5 + 8 + 6) / 6 = 40/6 ~ 6.67
Risultato:
La media è 6.67.
Esercizio 2: Trova la Moda
Problema:
Dataset: 12, 15, 14, 15, 18, 15, 14, 17
Svolgimento:
Osserviamo le frequenze:
12 compare 1 volta
14 compare 2 volte
15 compare 3 volte ✅
17 compare 1 volta
18 compare 1 volta
Risultato:
La moda è 15 (è il numero che compare più spesso).
Esercizio 3: Determina la Mediana
Problema:
Numeri dati: 25, 18, 30, 22, 27, 19, 24
Svolgimento:
1) Ordiniamo i dati in ordine crescente: 18, 19, 22, 24, 25, 27, 30
2) Il numero centrale è 24 (dato che ci sono 7 elementi, la mediana è il quarto valore).
Risultato:
La mediana è 24.
Esercizio 4: Applicazione Avanzata
Problema:
Dataset: 40, 41, 42, 41, 43, 41, 42, 40, 42, 44, 40. Trova Moda, Media e Mediana
Svolgimento:
1) Troviamo la moda
Osserviamo le frequenze:
40 compare 3 volte
41 compare 3 volte
42 compare 3 volte
43 compare 1 volta
44 compare 1 volta
Poiché 40, 41 e 42 compaiono tutte e tre lo stesso numero di volte, abbiamo un dataset multimodale con tre mode: 40, 41 e 42.
2) Calcoliamo la media
Media = (40 + 41 + 42 + 41 + 43 + 41 + 42 + 40 + 42 + 44 + 40) / 11 = 436/11 ~ 39.64
3) Troviamo la mediana
Ordiniamo i numeri: 40, 40, 40, 41, 41, 41, 42, 42, 42, 43, 44
Il valore centrale (il 6° elemento) è 41.
Risultato:
La moda è 40, 41 e 42.
La media è 39.64.
La mediana è 41.
Curiosità e Applicazioni
Media Ponderata: Quando i Valori Hanno Pesi Diversi
Se alcuni dati sono più importanti di altri, usiamo la media ponderata.
Media ponderata = (x1w1 + x2w2 + ... + xnwn) / w1 + w2 + ... + wn
Esempio tipico: calcolo del voto di maturità, dove le materie hanno pesi diversi.
Analisi dei Dati: Oltre la Tendenza Centrale
Varianza e deviazione standard misurano la dispersione dei dati.
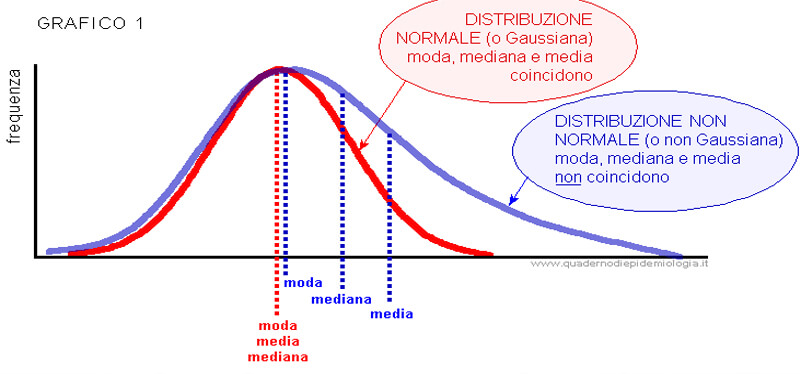
Distribuzione normale (curva a campana) è fondamentale per probabilità e statistica.
Conclusioni
Abbiamo esplorato media, moda e mediana, strumenti essenziali per l'analisi dei dati. Ora hai una comprensione completa e sai quando usare ciascuna misura.
👉 Continua ad allenarti con nuovi dati e situazioni reali! Hai altre domande o vuoi suggerire nuovi argomenti? Scrivici nei commenti! 🚀
Fonti: libri scolastici superiori

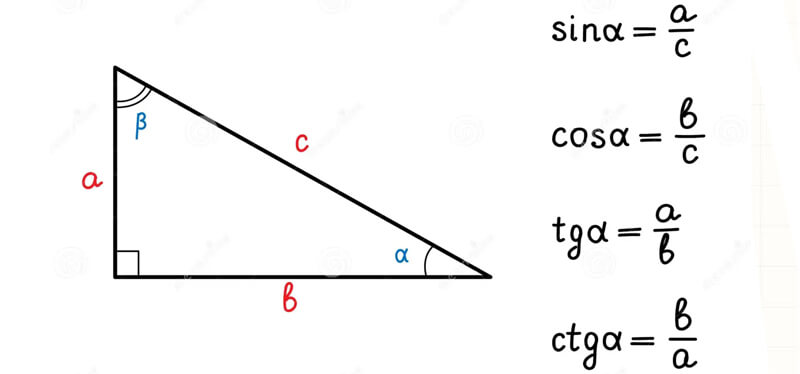 Identita trigonometriche - guida completa con esercizi risolti
Identita trigonometriche - guida completa con esercizi risolti
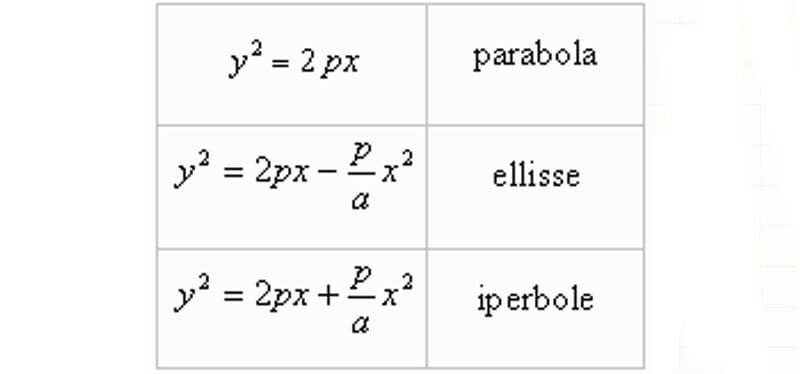 Equazione della parabola ellisse e iperbole - guida completa con esercizi risolti
Equazione della parabola ellisse e iperbole - guida completa con esercizi risolti
 Equazione della circonferenza - guida completa con esercizi risolti
Equazione della circonferenza - guida completa con esercizi risolti
 Logaritmi ed esponenziali - guida completa con esercizi risolti
Logaritmi ed esponenziali - guida completa con esercizi risolti
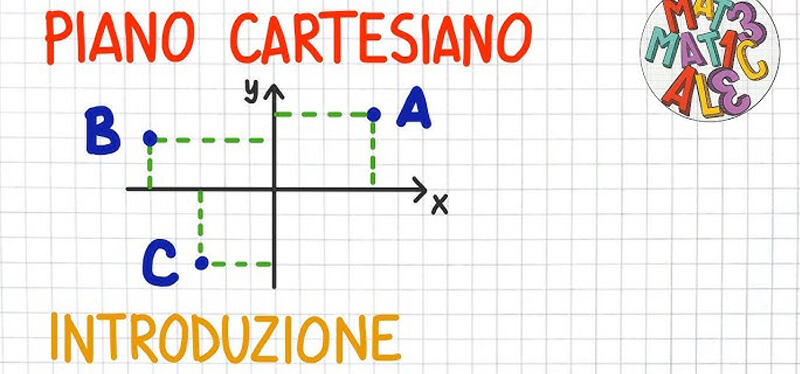 Il piano cartesiano - guida completa con esercizi risolti
Il piano cartesiano - guida completa con esercizi risolti
 La retta - equazione e coefficiente angolare - guida completa con esercizi risolti
La retta - equazione e coefficiente angolare - guida completa con esercizi risolti
 Teorema dei seni e teorema del coseno - guida completa con esercizi risolti
Teorema dei seni e teorema del coseno - guida completa con esercizi risolti
 Seno coseno e tangente - guida completa con esercizi risolti
Seno coseno e tangente - guida completa con esercizi risolti
 Radicali e numeri complessi - guida completa con esercizi risolti
Radicali e numeri complessi - guida completa con esercizi risolti
 Guida completa alle disequazioni di secondo grado - teoria esercizi e approfondimenti
Guida completa alle disequazioni di secondo grado - teoria esercizi e approfondimenti
 Guida completa alle equazioni di secondo grado - teoria esercizi e aprofondimenti
Guida completa alle equazioni di secondo grado - teoria esercizi e aprofondimenti
 Guida completa al calcolo delle probabilita - teoria esercizi e approfondimenti
Guida completa al calcolo delle probabilita - teoria esercizi e approfondimenti
 Le funzioni in matematica - guida completa con esercizi per tutti i livelli
Le funzioni in matematica - guida completa con esercizi per tutti i livelli
 Isometrie e similitudini - teoria esercizi e applicazioni
Isometrie e similitudini - teoria esercizi e applicazioni
 Introduzione alla geometria euclidea - teoria esercizi e approfondimenti
Introduzione alla geometria euclidea - teoria esercizi e approfondimenti
 Guida ai prodotti notevoli - teoria esercizi e applicazioni
Guida ai prodotti notevoli - teoria esercizi e applicazioni
 Alla scoperta delle disequazioni di primo grado - teoria ed esercizi
Alla scoperta delle disequazioni di primo grado - teoria ed esercizi
 Alla scoperta delle equazioni di primo grado - teoria ed esercizi
Alla scoperta delle equazioni di primo grado - teoria ed esercizi
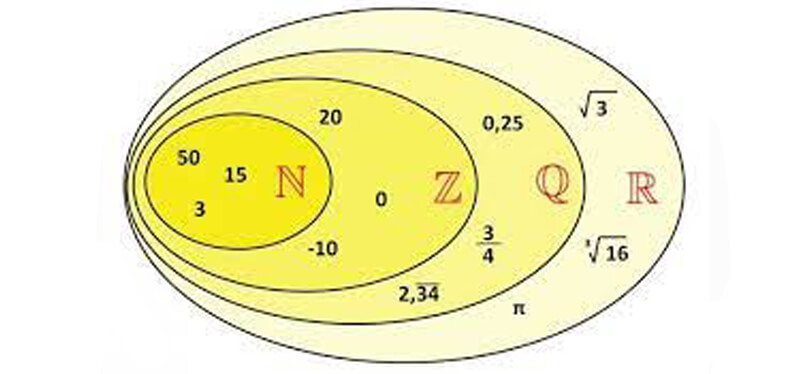 Numeri irrazionali - dalla teoria agli esercizi pratici
Numeri irrazionali - dalla teoria agli esercizi pratici