Equazione della Parabola, Ellisse e Iperbole: Guida Completa con Esercizi Risolti
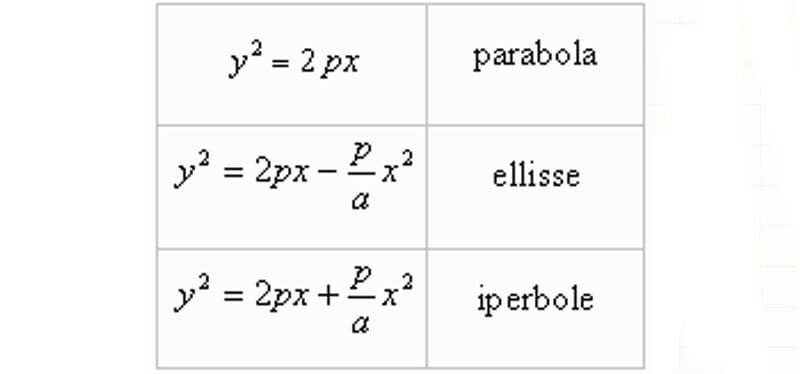
1) Introduzione
2) La Parabola: Definizione ed Equazione Generale
3) L'Ellisse: Definizione ed Equazione Generale
4) L'Iperbole: Definizione ed Equazione Generale
5) Confronto tra Parabola, Ellisse e Iperbole
6) Conclusioni
Introduzione
Le coniche sono curve geometriche fondamentali studiate in algebra e geometria analitica. Tra queste troviamo la parabola, l'ellisse e l'iperbole, che hanno applicazioni in fisica, ingegneria e astronomia.
In questa guida partiremo dalle basi e arriveremo a concetti avanzati, con esercizi risolti per ogni livello.
La Parabola: Definizione ed Equazione Generale
La parabola è il luogo dei punti equidistanti da un punto fisso detto fuoco e da una retta fissa detta direttrice.
Equazione generale della parabola con asse parallelo all'asse y
y = ax2 + bx + c
Il coefficiente a determina la concavità:
Se a > 0, la parabola è rivolta verso l'alto.
Se a < 0, la parabola è rivolta verso il basso.
Il vertice della parabola ha coordinate:
V(-b / 2a, (4ac - b2) / 4a)
L'asse di simmetria è la retta verticale:
x = -b / 2a
Il fuoco e la direttrice sono dati da:
F(-b / 2a, (1 - Δ) / 4a), y = (1 + Δ) / 4a
dove Δ = b2 - 4ac è il discriminante.
Esercizio 1 - Trovare il Vertice di una Parabola
Trova il vertice della parabola:
y = 2x2 - 4x + 1
Soluzione:
Usiamo la formula del vertice:
xV = -4 / 2(2) = 4 / 4 = 1
yY = (4(2)(1) - (-4)2) / 4(2) = (8 - 16) / 8 = -1
Quindi, il vertice è V(1, −1).
L'Ellisse: Definizione ed Equazione Generale
L'ellisse è il luogo dei punti la cui somma delle distanze da due punti fissi chiamati fuochi è costante.
Equazione generale dell'ellisse
x2 / a2 + y2 / b2 = 1
Se a > b, l'ellisse è orizzontale.
Se b > a, l'ellisse è verticale.
I fuochi hanno coordinate:
F1(-c, 0), F2(c, 0) con c = √a2 - b2
I vertici sono nei punti:
V1(-a, 0), V2(a, 0)
I semiassi sono a e b, con eccentricità:
e = c / a
Esercizio 2 - Determinare i Fuochi di un'Ellisse
Trova i fuochi dell'ellisse:
x2 / 25 + y2 / 9 = 1
Soluzione:
Qui a2 = 25 e b2 = 9, quindi a = 5 e b = 3.
Calcoliamo c:
c = √a2 - b2 = √25 - 9 = √16 = 4
Quindi i fuochi sono nei punti (−4, 0) e (4, 0).
L'Iperbole: Definizione ed Equazione Generale
L'iperbole è il luogo dei punti la cui differenza delle distanze da due fuochi fissi è costante.
Equazione generale dell'iperbole
x2 / a2 - y2 / b2 = 1
L'iperbole ha due rami separati.
I fuochi sono nei punti:
F1(-c, 0), F2(c, 0) con c = √a2 + b2
I vertici sono nei punti:
V1(-a, 0), V2(a, 0)
L'eccentricità è:
e = c / a
Le asintoti dell'iperbole sono le rette:
y = ± (b / a)x
Esercizio 3 - Determinare i Fuochi e gli Asintoti di un'Iperbole
Trova i fuochi e gli asintoti dell'iperbole:
x2 / 9 - y2 / 4 = 1
Soluzione:
Qui a2 = 9 e b2 = 4, quindi a = 3 e b = 2.
Calcoliamo c:
c = √a2 + b2 = √9 + 4 = √13
I fuochi sono nei punti (√−13, 0) e (√13, 0).
Gli asintoti sono dati da:
y = ± (b / a)x = ± (2 / 3)x
Confronto tra Parabola, Ellisse e Iperbole
Parabola
Equazione: y = ax2 + bx + c
Definizione: Luogo dei punti equidistanti da fuoco e direttrice
Fuochi: Uno
Asintoti: Nessuno
Ellisse
Equazione: x2 / a2 + y2 / b2 = 1
Definizione: Somma delle distanze dai fuochi costante
Fuochi: Due
Asintoti: Nessuno
Iperbole
Equazione: x2 / a2 - y2 / b2 = 1
Definizione: Differenza delle distanze dai fuochi costante
Fuochi: Due
Asintoti: Due
Conclusioni
Ora hai una panoramica completa sulla parabola, l'ellisse e l'iperbole, dalle basi alle applicazioni avanzate. Se vuoi approfondire, prova a risolvere nuovi esercizi e metti alla prova le tue conoscenze!
Fonti: libri scolastici superiori

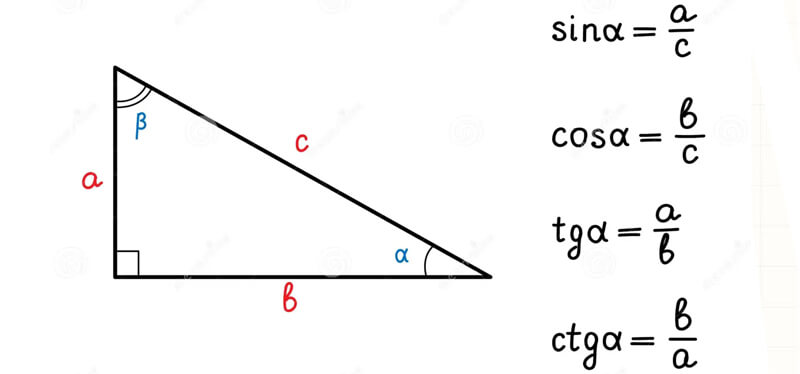 Identita trigonometriche - guida completa con esercizi risolti
Identita trigonometriche - guida completa con esercizi risolti
 Equazione della circonferenza - guida completa con esercizi risolti
Equazione della circonferenza - guida completa con esercizi risolti
 Logaritmi ed esponenziali - guida completa con esercizi risolti
Logaritmi ed esponenziali - guida completa con esercizi risolti
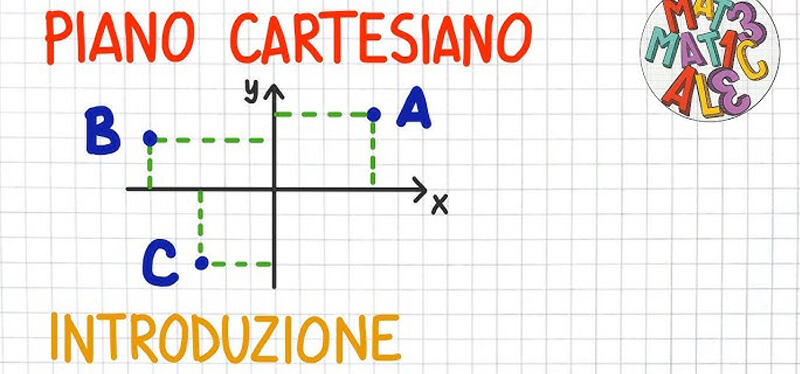 Il piano cartesiano - guida completa con esercizi risolti
Il piano cartesiano - guida completa con esercizi risolti
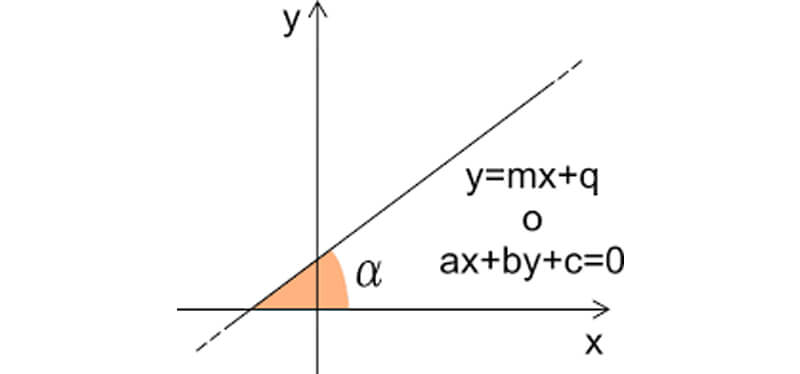 La retta - equazione e coefficiente angolare - guida completa con esercizi risolti
La retta - equazione e coefficiente angolare - guida completa con esercizi risolti
 Teorema dei seni e teorema del coseno - guida completa con esercizi risolti
Teorema dei seni e teorema del coseno - guida completa con esercizi risolti
 Seno coseno e tangente - guida completa con esercizi risolti
Seno coseno e tangente - guida completa con esercizi risolti
 Radicali e numeri complessi - guida completa con esercizi risolti
Radicali e numeri complessi - guida completa con esercizi risolti
 Guida completa alle disequazioni di secondo grado - teoria esercizi e approfondimenti
Guida completa alle disequazioni di secondo grado - teoria esercizi e approfondimenti
 Guida completa alle equazioni di secondo grado - teoria esercizi e aprofondimenti
Guida completa alle equazioni di secondo grado - teoria esercizi e aprofondimenti
 Guida completa al calcolo delle probabilita - teoria esercizi e approfondimenti
Guida completa al calcolo delle probabilita - teoria esercizi e approfondimenti
 Media moda e mediana - la statistica per tutti
Media moda e mediana - la statistica per tutti
 Le funzioni in matematica - guida completa con esercizi per tutti i livelli
Le funzioni in matematica - guida completa con esercizi per tutti i livelli
 Isometrie e similitudini - teoria esercizi e applicazioni
Isometrie e similitudini - teoria esercizi e applicazioni
 Introduzione alla geometria euclidea - teoria esercizi e approfondimenti
Introduzione alla geometria euclidea - teoria esercizi e approfondimenti
 Guida ai prodotti notevoli - teoria esercizi e applicazioni
Guida ai prodotti notevoli - teoria esercizi e applicazioni
 Alla scoperta delle disequazioni di primo grado - teoria ed esercizi
Alla scoperta delle disequazioni di primo grado - teoria ed esercizi
 Alla scoperta delle equazioni di primo grado - teoria ed esercizi
Alla scoperta delle equazioni di primo grado - teoria ed esercizi
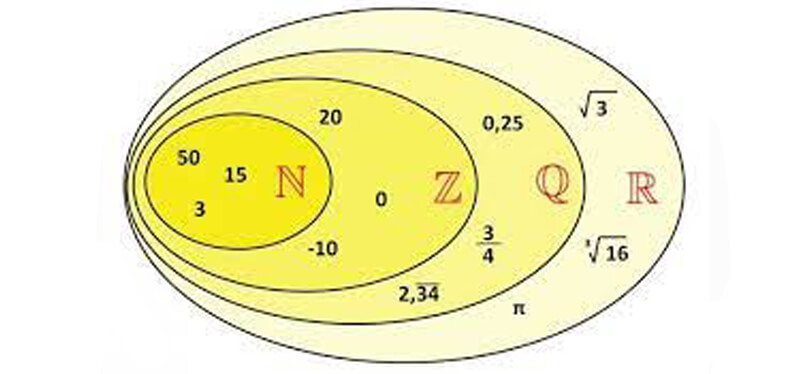 Numeri irrazionali - dalla teoria agli esercizi pratici
Numeri irrazionali - dalla teoria agli esercizi pratici