Guida Completa alle Disequazioni di Secondo Grado: Teoria, Esercizi e Approfondimenti

1) Introduzione
2) Cosa sono le Disequazioni di Secondo Grado?
3) Metodo Generale di Risoluzione
4) Esercizi Pratici
5) Approfondimento
6) Conclusioni
Introduzione
Le disequazioni di secondo grado sono un argomento fondamentale dell'algebra e trovano applicazione in fisica, economia e scienze applicate.
In questo articolo ti guiderò passo dopo passo, partendo dalle basi fino a esercizi avanzati e trucchi per risolverle in modo rapido ed efficace.
Cosa sono le Disequazioni di Secondo Grado?
Una disequazione di secondo grado è un'inequazione della forma: ax2 + bx + c relazione 0 dove:
- a, b, c sono numeri reali con a ≠ 0,
- x è l'incognita,
- la relazione può essere uno tra i seguenti simboli:
> (maggiore di)
≥ (maggiore o uguale a)
< (minore di)
≤ (minore o uguale a)
Esempi di Disequazioni di Secondo Grado
x2 −4x + 3 > 0
x2 +2x ≤ 0
2x2 −3x − 5 ≥ 0
L'obiettivo è trovare gli intervalli di x che soddisfano la disequazione.
Metodo Generale di Risoluzione
Passaggio 1: Risolvere l'Equazione Associata
Prima di risolvere una disequazione, risolviamo l'equazione associata: ax2 +bx + c = 0
Le soluzioni di questa equazione dividono la retta reale in intervalli.
Passaggio 2: Studio del Segno del Trinomio
Analizziamo il segno di ax2 + bx + c in ciascun intervallo e determiniamo quando è positivo o negativo.
Il metodo più rapido è usare la tabella dei segni.
Esercizi Pratici
Esercizio 1: Disequazione con Delta Positivo
Problema:
Risolvi la disequazione: x2 −5x + 6 > 0
Svolgimento:
Passaggio 1: Risolviamo l'equazione associata x2 −5x + 6 = 0
Scomponiamo in fattori: (x − 2)(x − 3) = 0
Quindi le soluzioni sono: x1 = 2, x2 = 3
Passaggio 2: Studio del segno
Il trinomio si annulla per x = 2 e x = 3.
Essendo un parabola con a > 0, il segno della funzione è:
Positivo per x < 2 e x > 3.
Negativo tra 2 e 3
Passaggio 3: Scrittura della Soluzione
Poiché cerchiamo dove la funzione è maggiore di 0, la soluzione è: x ∈ (-∞, 2) U (3, +∞)
Risultato:
x < 2 oppure x > 3.
Esercizio 2: Disequazione con Delta Zero
Problema:
Risolvi la disequazione: x2 −4x + 4 ≤ 0
Svolgimento:
Passaggio 1: Risolviamo l'equazione associata x2 −4x + 4 = 0
Scomponiamo in fattori: (x - 2)(x - 2) = 0 => x = 2
Passaggio 2: Studio del segno
La parabola ha un unico zero doppio in x = 2 e non cambia segno: è sempre positiva o nulla.
Passaggio 3: Scrittura della Soluzione
Cerchiamo dove è minore o uguale a zero, quindi l'unico valore accettabile è: x = 2
Risultato:
x = 2.
Esercizio 3: Disequazione con Delta Negativo
Problema:
Risolvi la disequazione: x2 + x + 1 > 0
Svolgimento:
Passaggio 1: Risolviamo l'equazione associata x2 + x + 1 = 0
Calcoliamo il discriminante: Δ = 12 −4(1)(1) = 1 - 4 = −3
Poiché Δ < 0, l'equazione non ha soluzioni reali.
Passaggio 2: Studio del segno
La parabola è sempre positiva perché a = 1 > 0.
Passaggio 3: Scrittura della Soluzione
Poiché la parabola è sempre positiva, la soluzione è: ∀x ∈ R
Risultato:
x può assumere qualsiasi valore reale.
Approfondimento
Metodo Alternativo: Segno del Coefficiente a
Un trucco per capire il segno della parabola è osservare il coefficiente di x2:
Se a > 0, la parabola è rivolta verso l'alto.
Se a < 0, la parabola è rivolta verso il basso.
Disequazioni con Denominatore
Le disequazioni frazionarie contengono il termine x anche al denominatore. In questi casi:
Troviamo gli zeri di numeratore e denominatore.
Studiamo il segno della frazione.
Escludiamo i valori che annullano il denominatore.
Esempio:
(x - 1) / (x + 2) > 0
x − 1 = 0 => x = 1
x + 2 = 0 => x = −2 (da escludere)
Studiamo il segno nei vari intervalli e scriviamo la soluzione finale.
Conclusioni
Le disequazioni di secondo grado sono fondamentali per la matematica e le loro applicazioni spaziano dalla fisica alla finanza.
Con questo metodo passo passo, puoi risolvere ogni tipo di disequazione in modo sicuro e veloce.
Fonti: libri scolastici superiori

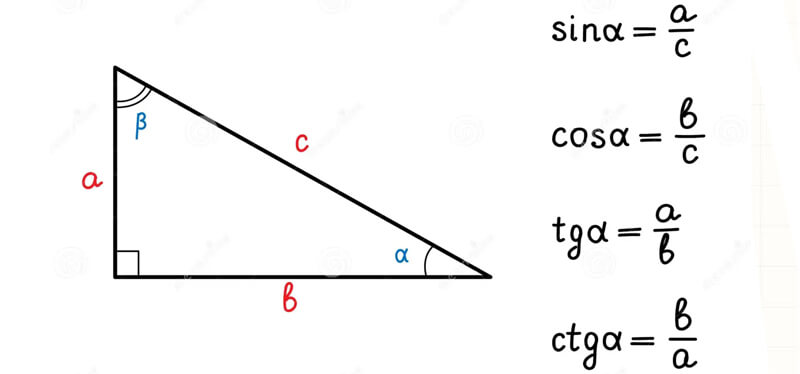 Identita trigonometriche - guida completa con esercizi risolti
Identita trigonometriche - guida completa con esercizi risolti
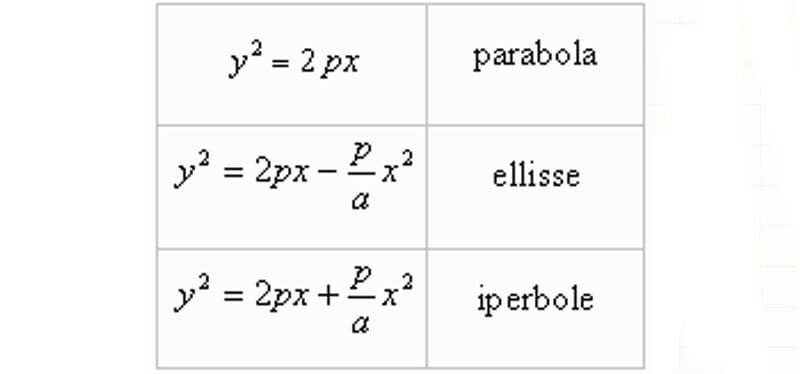 Equazione della parabola ellisse e iperbole - guida completa con esercizi risolti
Equazione della parabola ellisse e iperbole - guida completa con esercizi risolti
 Equazione della circonferenza - guida completa con esercizi risolti
Equazione della circonferenza - guida completa con esercizi risolti
 Logaritmi ed esponenziali - guida completa con esercizi risolti
Logaritmi ed esponenziali - guida completa con esercizi risolti
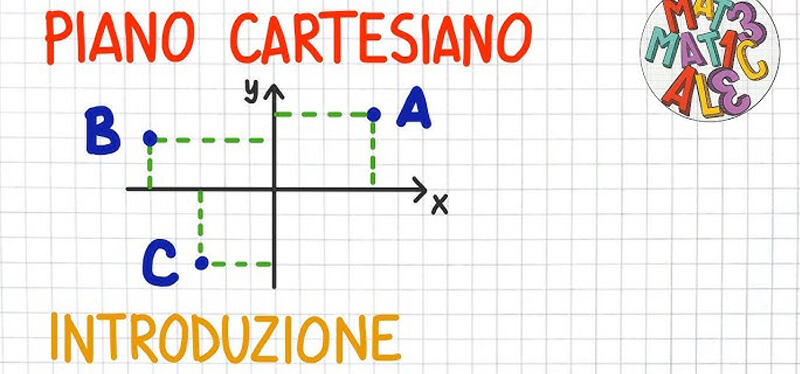 Il piano cartesiano - guida completa con esercizi risolti
Il piano cartesiano - guida completa con esercizi risolti
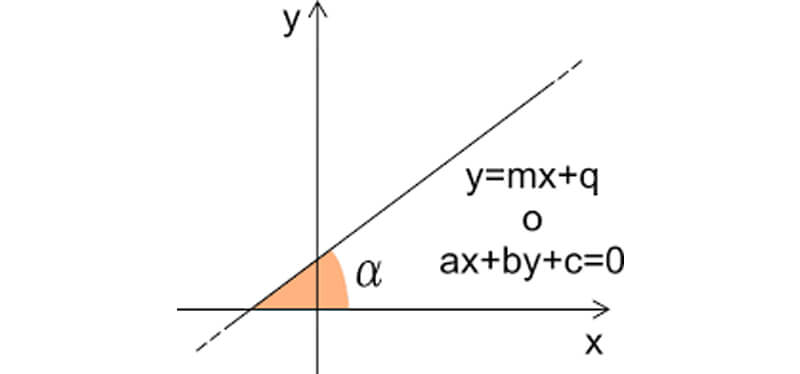 La retta - equazione e coefficiente angolare - guida completa con esercizi risolti
La retta - equazione e coefficiente angolare - guida completa con esercizi risolti
 Teorema dei seni e teorema del coseno - guida completa con esercizi risolti
Teorema dei seni e teorema del coseno - guida completa con esercizi risolti
 Seno coseno e tangente - guida completa con esercizi risolti
Seno coseno e tangente - guida completa con esercizi risolti
 Radicali e numeri complessi - guida completa con esercizi risolti
Radicali e numeri complessi - guida completa con esercizi risolti
 Guida completa alle equazioni di secondo grado - teoria esercizi e aprofondimenti
Guida completa alle equazioni di secondo grado - teoria esercizi e aprofondimenti
 Guida completa al calcolo delle probabilita - teoria esercizi e approfondimenti
Guida completa al calcolo delle probabilita - teoria esercizi e approfondimenti
 Media moda e mediana - la statistica per tutti
Media moda e mediana - la statistica per tutti
 Le funzioni in matematica - guida completa con esercizi per tutti i livelli
Le funzioni in matematica - guida completa con esercizi per tutti i livelli
 Isometrie e similitudini - teoria esercizi e applicazioni
Isometrie e similitudini - teoria esercizi e applicazioni
 Introduzione alla geometria euclidea - teoria esercizi e approfondimenti
Introduzione alla geometria euclidea - teoria esercizi e approfondimenti
 Guida ai prodotti notevoli - teoria esercizi e applicazioni
Guida ai prodotti notevoli - teoria esercizi e applicazioni
 Alla scoperta delle disequazioni di primo grado - teoria ed esercizi
Alla scoperta delle disequazioni di primo grado - teoria ed esercizi
 Alla scoperta delle equazioni di primo grado - teoria ed esercizi
Alla scoperta delle equazioni di primo grado - teoria ed esercizi
 Numeri irrazionali - dalla teoria agli esercizi pratici
Numeri irrazionali - dalla teoria agli esercizi pratici