Teorema dei Seni e Teorema del Coseno: Guida Completa con Esercizi Risolti

---

---

1) Introduzione
2) Il Teorema dei Seni: Definizione e Applicazione
3) Il Teorema del Coseno: Definizione e Applicazione
4) Confronto tra i due Teoremi: Quale Usare?
5) Applicazioni
6) Conclusioni

---

I triangoli sono una delle figure geometriche più studiate in matematica, e due strumenti fondamentali per risolverli sono il teorema dei seni e il teorema del coseno. Questi teoremi permettono di calcolare lati e angoli in triangoli qualsiasi, anche quando il teorema di Pitagora non è applicabile.

In questa guida, partiremo dalle basi e arriveremo a concetti avanzati, con esercizi risolti per tutti i livelli.

---

Il teorema dei seni stabilisce che in qualsiasi triangolo (non solo nei triangoli rettangoli) i rapporti tra la lunghezza di un lato e il seno del suo angolo opposto sono uguali:
a / sinA = b / sinB = c / sinC

Dove:
a,b,c sono i lati del triangolo
A,B,C sono gli angoli opposti ai rispettivi lati

Quando usare il Teorema dei Seni?
Quando si conoscono un lato e due angoli (caso ALA, angolo-lato-angolo).
Quando si conoscono due lati e un angolo opposto a uno di essi (caso LAL, lato-angolo-lato).
Esercizio 1 - Trovare un lato con il Teorema dei Seni

Dati:
Un triangolo ha:
A = 40
B = 60
a = 10 cm
Troviamo il lato b.

Soluzione:
1) Troviamo il terzo angolo:
C = 180° − A − B = 180° − 40° − 60° = 80°
2) Applichiamo il teorema dei seni:
a / sinA = b / sinB
10 / sin40° = b / sin60°
b = (10 · sin60°) / sin40°
b ~ (10 · 0.866) / 0.643 ~ 13.5 cm

---

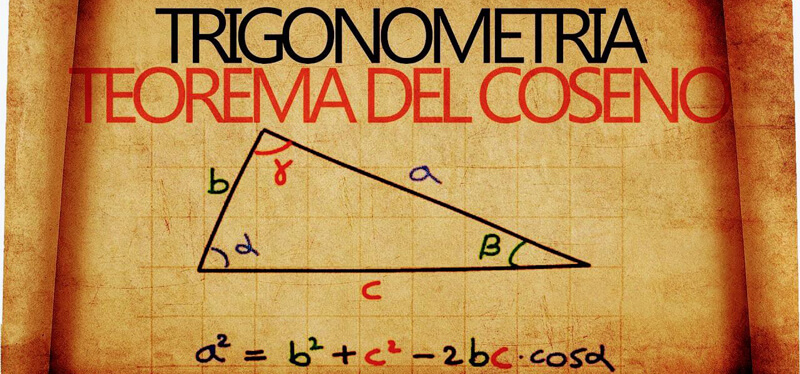
Il teorema del coseno è una generalizzazione del teorema di Pitagora e si applica a qualsiasi triangolo. Esso afferma che:
c² = a² + b² −2abcosC
a² = b² + c² −2bccosA
b² = a² + c² −2accosB

Quando usare il Teorema del Coseno?
Quando si conoscono due lati e l'angolo tra di essi (caso LAL, lato-angolo-lato).

Esercizio 2 - Trovare un lato con il Teorema del Coseno
Dati: Un triangolo ha:
a = 7 cm
b = 5 cm
C = 60°
Troviamo c.

Soluzione:
Quando si conoscono tutti e tre i lati e vogliamo trovare un angolo (caso LLL, lato-lato-lato).
c² = a² + b² −2abcosC
c² = 7² + 5² −2(7)(5)cos60°
c² = 49 + 25 − 70 · 0.5
c² = 74 − 35 = 39
c = √39 ~ 6.24 cm

Esercizio 3 - Trovare un angolo con il Teorema del Coseno
Dati: Un triangolo ha:
a = 6 cm
b = 8 cm
c = 10 cm
Troviamo l'angolo C.

Soluzione:
cosC = a² + b² - c² / 2ab
cosC = 6² + 8² - 10² / 2(6)(8)
cosC = (36 + 64 − 100) / 96 = 0 / 96 = 0
C = cos⁻¹(0) = 90°
Il triangolo è rettangolo!

---

Situazione:

Due angoli e un lato => Usiamo il Teorema dei Seni
Due lati e un angolo opposto a uno di essi => Usiamo il Teorema dei Seni
Due lati e l’angolo compreso => Usiamo il Teorema del Coseno
Tre lati noti => Usiamo il Teorema del Coseno

---

Questi teoremi trovano applicazione in:

✅ Fisica: calcoli di forze e traiettorie
✅ Ingegneria: costruzioni e progettazione di strutture
✅ Astronomia: calcolo delle distanze tra stelle
✅ Navigazione: determinazione di rotte e posizioni

---

Ora hai una panoramica completa sui teoremi dei seni e del coseno, dalle basi alle applicazioni avanzate. Se vuoi approfondire, continua a esercitarti con problemi più complessi e scopri come questi teoremi vengono utilizzati nel mondo reale!

Utenti più Affidabili:

Ultimi Articoli:

Ultimi Commenti: