Alla Scoperta delle Disequazioni di Primo Grado: Teoria ed Esercizi

1) Introduzione
2) Video Riassuntivo
3) Introduzione alle Disequazioni di Primo Grado
4) Come Risolvere una Disequazione di Primo Grado
5) Esercizi Pratici: Dalle Basi agli Approfondimenti
6) Applicazioni ed Approfondimenti delle Disequazioni di Primo Grado
7) Conclusioni
Introduzione
Le disequazioni di primo grado rappresentano un concetto fondamentale dell'algebra e trovano applicazione in numerosi contesti reali, dalla fisica all'economia. In questo articolo, esploreremo il loro significato, le tecniche risolutive e vedremo esercizi per tutti i livelli, dalla base fino a casi più avanzati.
Video Riassuntivo
Introduzione alle Disequazioni di Primo Grado
Cosa Sono le Disequazioni di Primo Grado?
Una disequazione di primo grado è un'espressione algebrica in cui la variabile compare elevata alla prima potenza e che, invece di un segno di uguaglianza (=), presenta un segno di disuguaglianza, ovvero:
< (minore)
> (maggiore)
≤ (minore o uguale)
≥ (maggiore o uguale)
Esempio di Disequazione:
3x −5 < 10
L'obiettivo è trovare i valori della variabile x che soddisfano la disequazione.
Come Risolvere una Disequazione di Primo Grado
Il metodo di risoluzione è simile a quello delle equazioni di primo grado, con una differenza fondamentale: se moltiplichiamo o dividiamo per un numero negativo, dobbiamo invertire il segno della disuguaglianza.
Passaggi Generali per la Risoluzione:
1) Isoliamo la variabile sul lato sinistro.
2) Trasferiamo i termini costanti al lato opposto.
3) Dividiamo o moltiplichiamo per il coefficiente della variabile.
4) Se moltiplichiamo o dividiamo per un numero negativo, invertiamo il segno della disuguaglianza.
Esercizi Pratici: Dalle Basi agli Approfondimenti
Esercizio 1: Disequazione Semplice
Problema:
Risolvi la disequazione: 2x +3 > 7
Svolgimento:
1) Sottraiamo 3 da entrambi i membri: 2x > 4
2) Dividiamo per 2: x > 2
Risultato:
x > 2 significa che tutti i valori di x maggiori di 2 soddisfano la disequazione.
Rappresentazione Grafica sulla Retta dei Numeri:
Tracciamo una linea orizzontale e segnamo il numero 2.
Poiché x > 2, disegniamo un pallino vuoto su 2 e una freccia che va verso destra.
Esercizio 2: Disequazione con Coefficienti Negativi
Problema:
Risolvi la disequazione: −3x +4 ≤ 1
Svolgimento:
1) Sottraiamo 4 da entrambi i membri: −3x ≤ −3
2) Dividiamo per -3 e cambiamo il segno della disuguaglianza: x ≥ 1
Risultato:
x ≥ 1 significa che tutti i valori di x uguali o maggiori di 1 sono soluzioni.
Rappresentazione Grafica sulla Retta dei Numeri:
Tracciamo una linea orizzontale e segnamo il numero 1.
Poiché x ≥ 1, disegniamo un pallino pieno su 1 e una freccia che va verso destra.
Esercizio 3: Disequazione con Denominatori
Problema:
Risolvi la disequazione: x/2 -5 < 3
Svolgimento:
1) Sommiamo 5 a entrambi i membri: x/2 < 8
2) Moltiplichiamo entrambi i membri per 2: x < 16
Risultato:
x < 16 significa che tutti i valori di x minori di 16 soddisfano la disequazione.
Esercizio 4: Disequazione con un Sistema
Problema:
Risolvi il sistema di disequazioni (entrambe dentro la stessa {):
{ 2x −3 < 7
{ x +1 ≥ 4
Svolgimento:
1) Risolviamo la prima disequazione: 2x < 10 ⇒ x < 5
2) Risolviamo la seconda disequazione: x ≥ 3
Risultato:
3 ≤ x < 5
Rappresentazione Grafica:
Pallino pieno su 3 perché è incluso.
Pallino vuoto su 5 perché non è incluso.
Segmento tra 3 e 5.
Applicazioni ed Approfondimenti delle Disequazioni di Primo Grado
Le disequazioni non sono solo un esercizio scolastico! Ecco alcune applicazioni pratiche:
Finanza: Determinare i limiti di spesa per non superare un budget.
Fisica: Stabilire intervalli di valori in cui una grandezza è accettabile.
Economia: Definire condizioni di profitto minimo.
Approfondimenti e Curiosità
Le disequazioni con valori assoluti ampliano il concetto, portando a due disequazioni da risolvere separatamente.
Le disequazioni fratte contengono frazioni con variabili al denominatore e richiedono lo studio del dominio.
Le disequazioni quadratiche si basano su parabole e hanno due soluzioni distinte.
Conclusioni
Le disequazioni di primo grado sono un argomento fondamentale della matematica, utile sia negli studi teorici che nella vita quotidiana. Conoscere bene le tecniche risolutive permette di affrontare problemi più complessi con sicurezza.
Speriamo che questa guida ti abbia aiutato! Continua a esercitarti e, se vuoi, proponici nuovi problemi nei commenti! 😊📚
Fonti: libri scolastici superiori

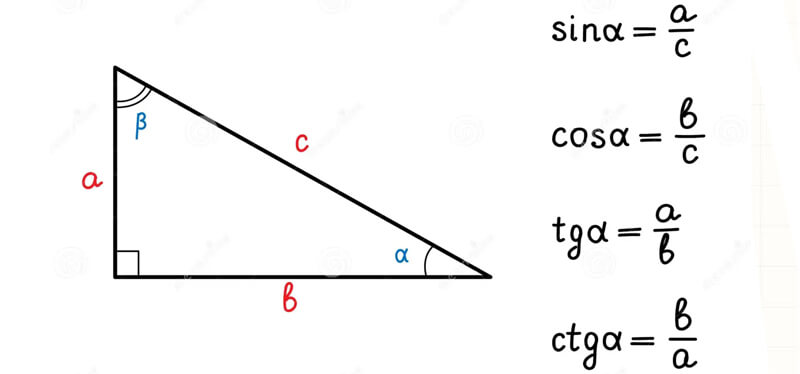 Identita trigonometriche - guida completa con esercizi risolti
Identita trigonometriche - guida completa con esercizi risolti
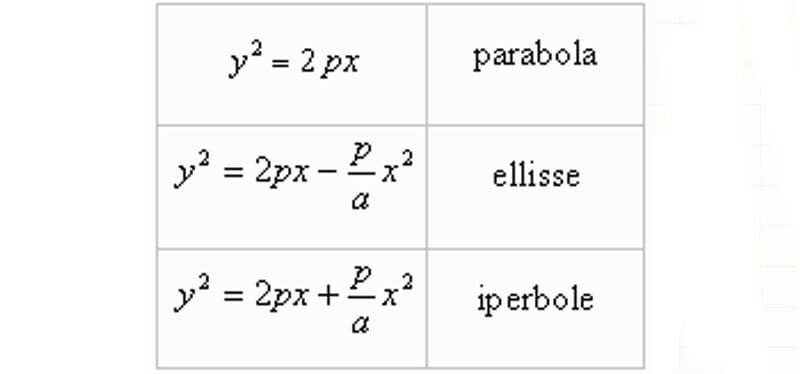 Equazione della parabola ellisse e iperbole - guida completa con esercizi risolti
Equazione della parabola ellisse e iperbole - guida completa con esercizi risolti
 Equazione della circonferenza - guida completa con esercizi risolti
Equazione della circonferenza - guida completa con esercizi risolti
 Logaritmi ed esponenziali - guida completa con esercizi risolti
Logaritmi ed esponenziali - guida completa con esercizi risolti
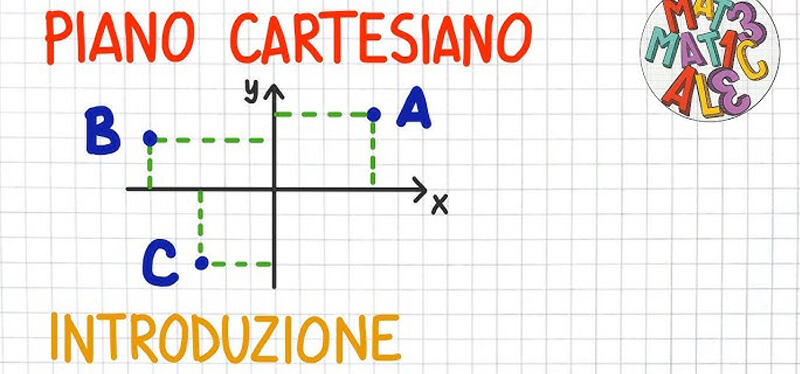 Il piano cartesiano - guida completa con esercizi risolti
Il piano cartesiano - guida completa con esercizi risolti
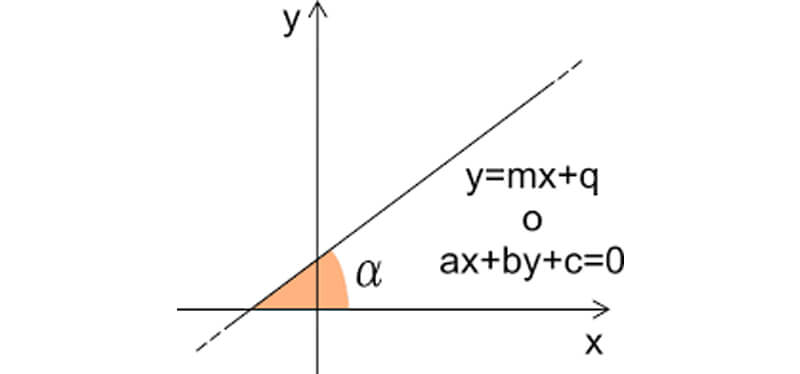 La retta - equazione e coefficiente angolare - guida completa con esercizi risolti
La retta - equazione e coefficiente angolare - guida completa con esercizi risolti
 Teorema dei seni e teorema del coseno - guida completa con esercizi risolti
Teorema dei seni e teorema del coseno - guida completa con esercizi risolti
 Seno coseno e tangente - guida completa con esercizi risolti
Seno coseno e tangente - guida completa con esercizi risolti
 Radicali e numeri complessi - guida completa con esercizi risolti
Radicali e numeri complessi - guida completa con esercizi risolti
 Guida completa alle disequazioni di secondo grado - teoria esercizi e approfondimenti
Guida completa alle disequazioni di secondo grado - teoria esercizi e approfondimenti
 Guida completa alle equazioni di secondo grado - teoria esercizi e aprofondimenti
Guida completa alle equazioni di secondo grado - teoria esercizi e aprofondimenti
 Guida completa al calcolo delle probabilita - teoria esercizi e approfondimenti
Guida completa al calcolo delle probabilita - teoria esercizi e approfondimenti
 Media moda e mediana - la statistica per tutti
Media moda e mediana - la statistica per tutti
 Le funzioni in matematica - guida completa con esercizi per tutti i livelli
Le funzioni in matematica - guida completa con esercizi per tutti i livelli
 Isometrie e similitudini - teoria esercizi e applicazioni
Isometrie e similitudini - teoria esercizi e applicazioni
 Introduzione alla geometria euclidea - teoria esercizi e approfondimenti
Introduzione alla geometria euclidea - teoria esercizi e approfondimenti
 Guida ai prodotti notevoli - teoria esercizi e applicazioni
Guida ai prodotti notevoli - teoria esercizi e applicazioni
 Alla scoperta delle equazioni di primo grado - teoria ed esercizi
Alla scoperta delle equazioni di primo grado - teoria ed esercizi
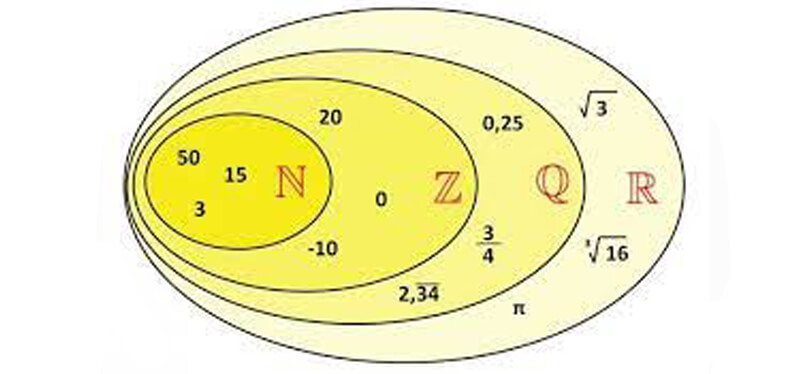 Numeri irrazionali - dalla teoria agli esercizi pratici
Numeri irrazionali - dalla teoria agli esercizi pratici