Le Funzioni in Matematica: Guida Completa con Esercizi per Tutti i Livelli
1) Introduzione
2) Cos'è una Funzione?
3) Esercizi Pratici: Dalle Basi agli Approfondimenti
4) Applicazioni Reali delle Funzioni
5) Conclusioni
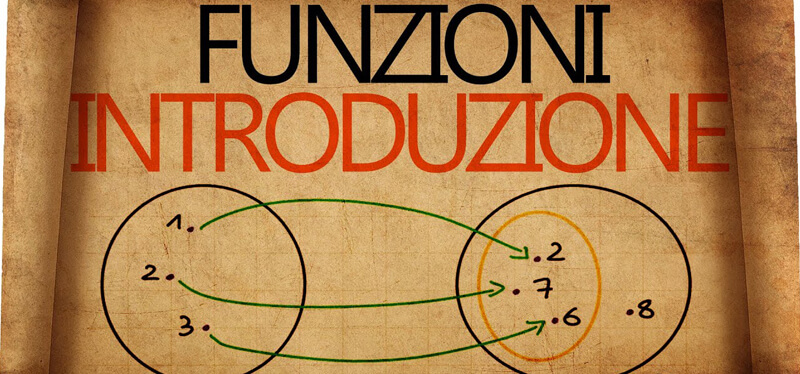
Introduzione
Le funzioni matematiche sono alla base di moltissimi concetti, dalla geometria all'analisi, fino alla programmazione e alla fisica. In questo articolo, esploreremo il concetto di funzione in modo chiaro e accessibile, partendo dalle basi fino ad arrivare a esercizi avanzati per gli esperti.
Che tu sia un principiante che vuole capire cosa sia una funzione o un esperto che desidera affinare le proprie abilità con problemi più complessi, qui troverai tutto ciò di cui hai bisogno.
Cos'è una Funzione?
Una funzione è una relazione tra due insiemi, in cui a ogni elemento del primo insieme (detto dominio) corrisponde uno e un solo elemento del secondo insieme (detto codominio).
Esempio Intuitivo: Il Distributore Automatico
Immagina un distributore automatico di bibite:
1) Premi il tasto "Coca-Cola" e ottieni una Coca-Cola.
2) Premi il tasto "Acqua" e ottieni una bottiglietta d'acqua.
Se ogni tasto restituisce una sola bevanda, il distributore rappresenta una funzione. Se premendo "Coca-Cola" potessi ottenere casualmente una Coca-Cola o un succo d'arancia, allora non sarebbe una funzione!
Definizione Matematica
Una funzione è una relazione f tra due insiemi A e B tale che ogni elemento di A ha un'unica immagine in B.
Si scrive: f: A -> B dove x (appartenente a A) viene trasformato in f(x) (appartenente a B).
Esempio Base di Funzione
f(x) = 2x + 3
Se scegliamo x = 1, otteniamo f(1) = 2(1) + 3 = 5.
Se scegliamo x = 4, otteniamo f(4) = 2(4) + 3 = 11.
In entrambi i casi, a ogni x corrisponde un solo valore di f(x), quindi questa è una funzione.
Tipi di Funzioni: Perché Sono Così Importanti?
Esistono tantissimi tipi di funzioni, ognuna con proprietà specifiche. Eccone alcune fondamentali:
Funzioni Lineari
Sono del tipo: f(x) = mx + q
Dove m è il coefficiente angolare e q è l'intercetta sull'asse y.
Esempio:
f(x) = 2x + 1 è una retta con inclinazione m = 2 e intercetta in q = 1.
Funzioni Quadratiche
Sono espresse come: f(x) = ax2 + bx + c
La loro rappresentazione grafica è una parabola.
Esempio: f(x) = x2 − 4x + 3.
Funzioni Esponenziali
Hanno la forma: f(x) = ax e crescono (o decrescono) molto rapidamente.
Esempio: f(x) = 2x raddoppia il valore per ogni incremento di x.
Funzioni Logaritmiche
Sono l'inverso delle esponenziali e hanno la forma: f(x) = loga(x)
Sono usate in informatica e scienze naturali.
Esercizi Pratici: Dalle Basi agli Approfondimenti
Esercizio 1: È una funzione?
Problema:
Quale di queste è una funzione?
1) A ogni persona viene assegnato un codice fiscale.
2) A ogni temperatura viene assegnata una sensazione diversa (freddo, caldo, tiepido).
Risultato:
Solo la prima è una funzione, perché a ogni persona corrisponde un solo codice fiscale. La seconda non è una funzione perché la stessa temperatura può essere percepita in modi diversi.
Esercizio 2: Valori di una funzione
Problema:
Data la funzione: f(x) = 3x − 2
Calcola f(0), f(2) e f(−1).
Risultato:
f(0) = 3(0) − 2 = −2
f(2) = 3(2) − 2 = 4
f(−1) = 3(−1) −2 = −5
Esercizio 3: Funzioni Inverse
Problema:
Trova la funzione inversa di: f(x) = (x − 3) / 2
Risultato:
Per trovare la funzione inversa, risolviamo per x:
1) Scambiamo x e y: x = (y - 3) / 2
2) Moltiplichiamo entrambi i lati per 2: 2x = y − 3
3) Aggiungiamo 3 a entrambi i lati: y = 2x + 3
La funzione inversa è: f−1(x) = 2x + 3
Applicazioni Reali delle Funzioni
Le funzioni non servono solo nei libri di matematica, ma trovano applicazione in tantissimi settori:
Economia: la funzione del costo totale in base alla quantità prodotta.
Fisica: la legge del moto rettilineo uniforme s(t) = vt + s0
Informatica: le funzioni sono alla base dei linguaggi di programmazione.
Conclusioni
Le funzioni sono un concetto essenziale in matematica e in tantissime discipline scientifiche. Se vuoi padroneggiare questo argomento:
✅ Esercitati con vari tipi di funzioni
✅ Disegna i grafici per visualizzare meglio i concetti
✅ Studia le funzioni inverse per comprendere le relazioni tra insiemi
Vuoi metterti alla prova? Risolvi questi esercizi aggiuntivi e condividi le tue soluzioni nei commenti!
1) Determina se la relazione x2 + y2 = 1 è una funzione.
2) Trova il dominio della funzione f(x) = 1 / (x − 2)
3) Risolvi f(x) = 5x + 7 per x = −3.
Fonti: libri scolastici superiori

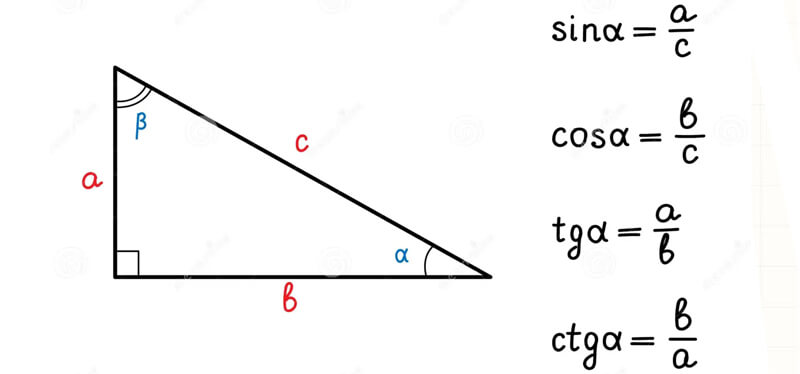 Identita trigonometriche - guida completa con esercizi risolti
Identita trigonometriche - guida completa con esercizi risolti
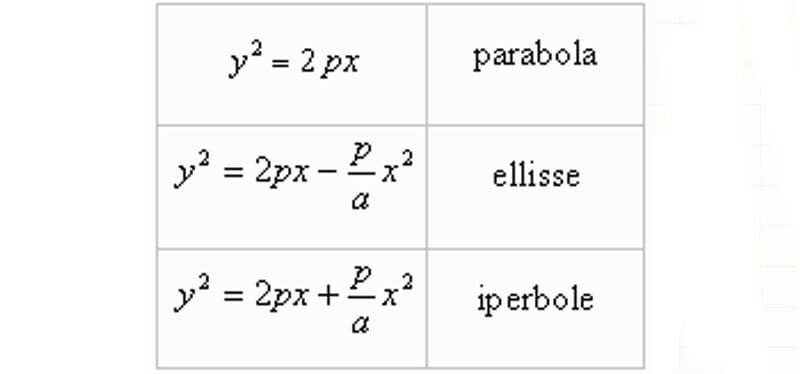 Equazione della parabola ellisse e iperbole - guida completa con esercizi risolti
Equazione della parabola ellisse e iperbole - guida completa con esercizi risolti
 Equazione della circonferenza - guida completa con esercizi risolti
Equazione della circonferenza - guida completa con esercizi risolti
 Logaritmi ed esponenziali - guida completa con esercizi risolti
Logaritmi ed esponenziali - guida completa con esercizi risolti
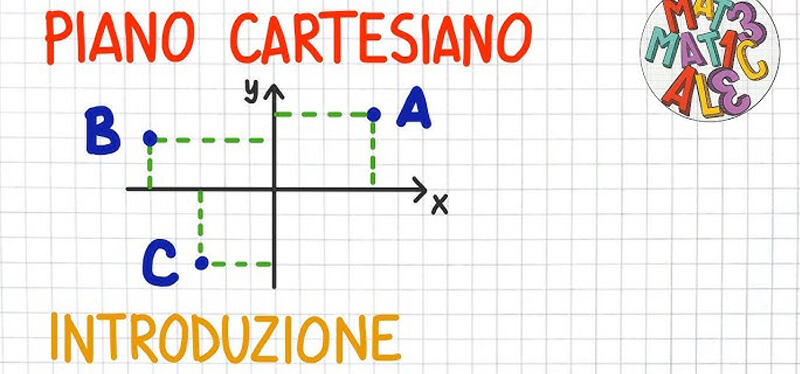 Il piano cartesiano - guida completa con esercizi risolti
Il piano cartesiano - guida completa con esercizi risolti
 La retta - equazione e coefficiente angolare - guida completa con esercizi risolti
La retta - equazione e coefficiente angolare - guida completa con esercizi risolti
 Teorema dei seni e teorema del coseno - guida completa con esercizi risolti
Teorema dei seni e teorema del coseno - guida completa con esercizi risolti
 Seno coseno e tangente - guida completa con esercizi risolti
Seno coseno e tangente - guida completa con esercizi risolti
 Radicali e numeri complessi - guida completa con esercizi risolti
Radicali e numeri complessi - guida completa con esercizi risolti
 Guida completa alle disequazioni di secondo grado - teoria esercizi e approfondimenti
Guida completa alle disequazioni di secondo grado - teoria esercizi e approfondimenti
 Guida completa alle equazioni di secondo grado - teoria esercizi e aprofondimenti
Guida completa alle equazioni di secondo grado - teoria esercizi e aprofondimenti
 Guida completa al calcolo delle probabilita - teoria esercizi e approfondimenti
Guida completa al calcolo delle probabilita - teoria esercizi e approfondimenti
 Media moda e mediana - la statistica per tutti
Media moda e mediana - la statistica per tutti
 Isometrie e similitudini - teoria esercizi e applicazioni
Isometrie e similitudini - teoria esercizi e applicazioni
 Introduzione alla geometria euclidea - teoria esercizi e approfondimenti
Introduzione alla geometria euclidea - teoria esercizi e approfondimenti
 Guida ai prodotti notevoli - teoria esercizi e applicazioni
Guida ai prodotti notevoli - teoria esercizi e applicazioni
 Alla scoperta delle disequazioni di primo grado - teoria ed esercizi
Alla scoperta delle disequazioni di primo grado - teoria ed esercizi
 Alla scoperta delle equazioni di primo grado - teoria ed esercizi
Alla scoperta delle equazioni di primo grado - teoria ed esercizi
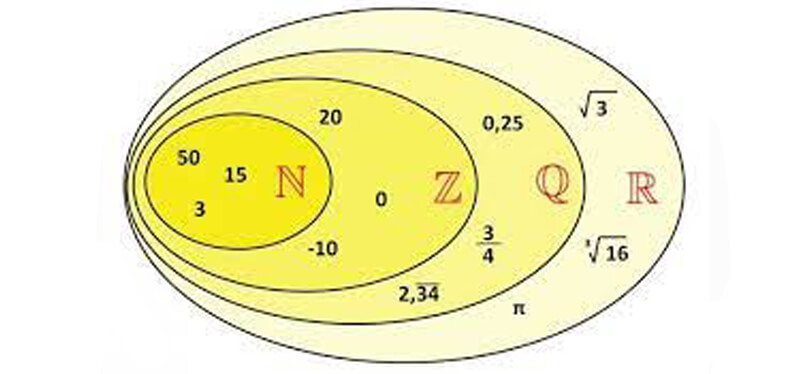 Numeri irrazionali - dalla teoria agli esercizi pratici
Numeri irrazionali - dalla teoria agli esercizi pratici