Alla Scoperta delle Potenze: Dalle Basi agli Esercizi Avanzati
1) Introduzione
2) Video Riassuntivo
3) Cos'è una Potenza?
4) Le Proprietà delle Potenze
5) Esercizi Pratici: Dal Principiante all'Esperto
6) Curiosità e Applicazioni
7) Conclusioni
Le potenze sono uno strumento fondamentale in matematica, capaci di semplificare calcoli, esprimere concetti in modo compatto e risolvere problemi complessi. In questo articolo esploreremo l'argomento a partire dalle basi, per poi approfondire le proprietà e proporre esercizi che spaziano da quelli per principianti fino a quelli più avanzati. Che tu sia alle prime armi o un vero esperto, troverai contenuti utili e stimolanti!
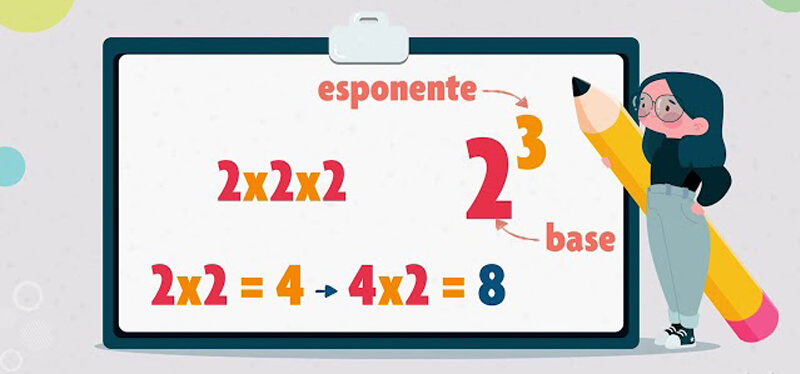
Una potenza si scrive nella forma an, dove:
- a è la base, ovvero il numero che viene moltiplicato per sé stesso.
- n è l'esponente, che indica quante volte moltiplichiamo la base per sé stessa.
Esempio Base:
34 = 3×3×3×3 = 81
Specialità delle Potenze:
Esponente Zero:
Per ogni numero Se a ≠ 0, si ha a0 = 1
Esponente Uno:
a1 = a, ovvero la potenza non modifica la base.
Esponenti Negativi:
a-n = 1/an Questi esponenti indicano l'inverso della potenza positiva.
Esponenti Frazionari:
a1/n rappresenta la radice n-esima di a, ad esempio: 91/2 = √9 = 3
Le potenze obbediscono a regole che permettono di semplificare e manipolare le espressioni:
Prodotto di Potenze con la Stessa Base:
am x an = am+n
Esempio:
23 x 24 = 23+4 = 27 = 128
Divisione di Potenze con la Stessa Base:
am / an = am-n
Esempio:
56 / 52 = 56-2 = 54 = 625
Potenza di una Potenza:
(am)n = am · n
Esempio:
(32)3 = 32 · 3 = 36 = 729
Prodotto di Potenze con lo Stesso Esponente:
an x bn = (a x b)n
Esempio:
23 x 33 = (2 x 3)3 = 63 = 216
Queste regole sono valide per ogni numero reale (con alcune eccezioni nei casi di 0) e costituiscono il fondamento per lavorare con espressioni esponenziali in modo rapido ed efficiente.
Esercizio 1: Semplificazione di un Prodotto
Problema:
Semplifica l'espressione:
23 x 25
Svolgimento:Utilizzando la regola del prodotto di potenze con la stessa base:
23 x 25 = 23 + 5 = 28
Risultato:28 = 256
Esercizio 2: Divisione di Potenze
Problema:
Calcola:
76 / 74
Svolgimento:Applicando la regola della divisione:
76 / 74 = 76-4 = 72
Risultato:72 = 49
Esercizio 3: Potenza di una Potenza
Problema:
Determina il valore di:
(43)2
Svolgimento:Utilizzando la regola della potenza di una potenza:
(43)2 = 43 x 2 = 46
Risultato:46 = 4096
Esercizio 4: Esercizio Avanzato con Esponenti Negativi e Frazionari
Problema:
Semplifica l'espressione:
5-2 x (53)1/2 / 51/2
Svolgimento:1) Calcoliamo la potenza di una potenza:
(53)1/2 = 53 x 1/2 = 53/2
2) Sostituiamo nell'espressione:5-2 x 53/2 / 51/2
3) Sommiamo gli esponenti nel numeratore:5-2 + 3/2 = 5-4/2 + 3/2 = 5-1/2
4) Applichiamo la divisione:5-1/2 / 51/2 = 5-1/2 -1/2 = 5-1
Risultato:5-1 = 1/5
Applicazioni Pratiche:
Le potenze vengono impiegate in numerosi ambiti:
Fisica: per esprimere grandezze che variano in modo esponenziale (come il decadimento radioattivo o la legge dell'attrazione gravitazionale).
Informatica: nella complessità algoritmica e nel calcolo dei bit.
Finanza: nel calcolo degli interessi composti.
Curiosità per gli Appassionati:
Crescita Esponenziale: La funzione esponenziale f(x) = ax (con a > 1) descrive fenomeni come la crescita della popolazione o il diffondersi di una malattia.
Logaritmi: Sono l'inverso delle potenze e offrono una via alternativa per risolvere equazioni esponenziali, rappresentando un ponte tra algebra e analisi.
Le potenze, pur sembrando un argomento semplice, rappresentano una componente essenziale della matematica che si applica in innumerevoli situazioni. Dal calcolo di una semplice espressione numerica alla modellazione di fenomeni complessi, la loro comprensione permette di affrontare con sicurezza sfide matematiche di ogni livello.
Che tu stia appena iniziando o che tu voglia approfondire aspetti avanzati, speriamo che questo articolo ti abbia fornito sia le basi teoriche che gli strumenti pratici per sfruttare al meglio il potere delle potenze. Continua a esercitarti, esplora le loro applicazioni e scopri come la matematica possa essere sorprendentemente elegante e utile nella vita quotidiana!
Buono studio e alla prossima scoperta matematica!

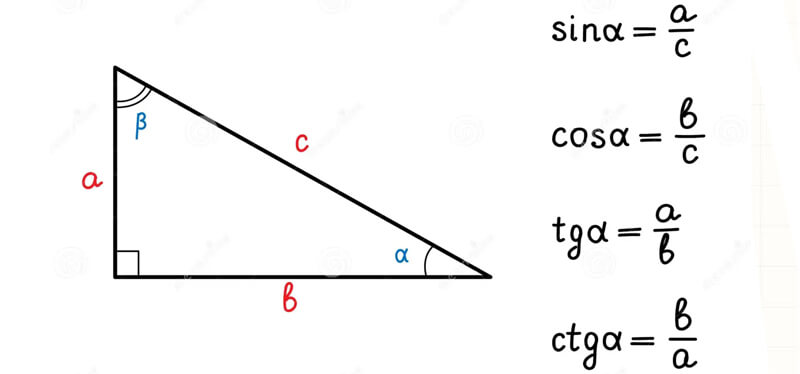 Identita trigonometriche - guida completa con esercizi risolti
Identita trigonometriche - guida completa con esercizi risolti
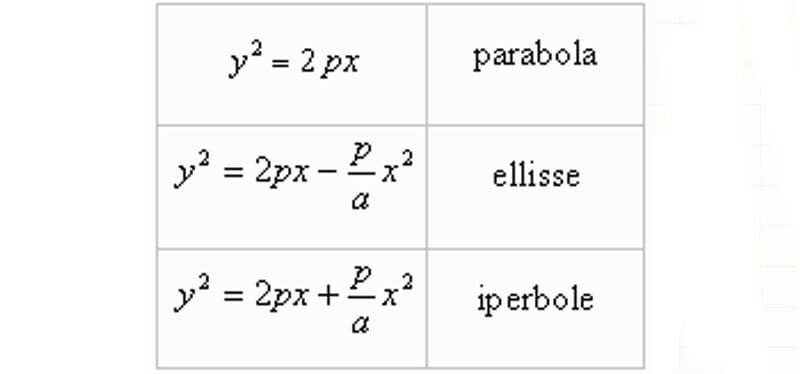 Equazione della parabola ellisse e iperbole - guida completa con esercizi risolti
Equazione della parabola ellisse e iperbole - guida completa con esercizi risolti
 Equazione della circonferenza - guida completa con esercizi risolti
Equazione della circonferenza - guida completa con esercizi risolti
 Logaritmi ed esponenziali - guida completa con esercizi risolti
Logaritmi ed esponenziali - guida completa con esercizi risolti
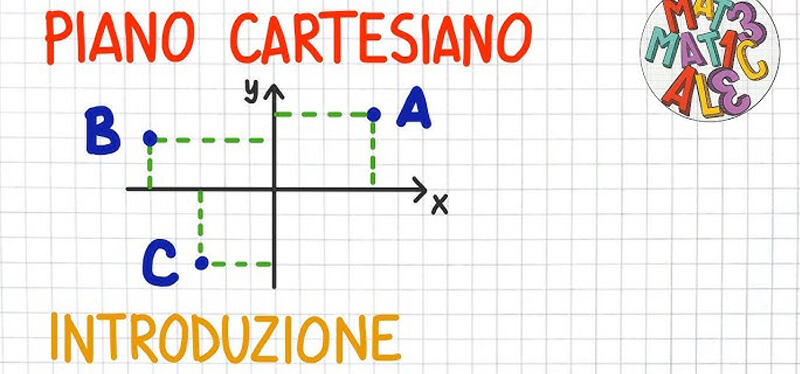 Il piano cartesiano - guida completa con esercizi risolti
Il piano cartesiano - guida completa con esercizi risolti
 La retta - equazione e coefficiente angolare - guida completa con esercizi risolti
La retta - equazione e coefficiente angolare - guida completa con esercizi risolti
 Teorema dei seni e teorema del coseno - guida completa con esercizi risolti
Teorema dei seni e teorema del coseno - guida completa con esercizi risolti
 Seno coseno e tangente - guida completa con esercizi risolti
Seno coseno e tangente - guida completa con esercizi risolti
 Radicali e numeri complessi - guida completa con esercizi risolti
Radicali e numeri complessi - guida completa con esercizi risolti
 Guida completa alle disequazioni di secondo grado - teoria esercizi e approfondimenti
Guida completa alle disequazioni di secondo grado - teoria esercizi e approfondimenti
 Guida completa alle equazioni di secondo grado - teoria esercizi e aprofondimenti
Guida completa alle equazioni di secondo grado - teoria esercizi e aprofondimenti
 Guida completa al calcolo delle probabilita - teoria esercizi e approfondimenti
Guida completa al calcolo delle probabilita - teoria esercizi e approfondimenti
 Media moda e mediana - la statistica per tutti
Media moda e mediana - la statistica per tutti
 Le funzioni in matematica - guida completa con esercizi per tutti i livelli
Le funzioni in matematica - guida completa con esercizi per tutti i livelli
 Isometrie e similitudini - teoria esercizi e applicazioni
Isometrie e similitudini - teoria esercizi e applicazioni
 Introduzione alla geometria euclidea - teoria esercizi e approfondimenti
Introduzione alla geometria euclidea - teoria esercizi e approfondimenti
 Guida ai prodotti notevoli - teoria esercizi e applicazioni
Guida ai prodotti notevoli - teoria esercizi e applicazioni
 Alla scoperta delle disequazioni di primo grado - teoria ed esercizi
Alla scoperta delle disequazioni di primo grado - teoria ed esercizi
 Alla scoperta delle equazioni di primo grado - teoria ed esercizi
Alla scoperta delle equazioni di primo grado - teoria ed esercizi
 Numeri irrazionali - dalla teoria agli esercizi pratici
Numeri irrazionali - dalla teoria agli esercizi pratici