L'Equazione della Circonferenza: Guida Completa con Esercizi Risolti
1) Introduzione
2) Definizione della Circonferenza
3) Equazione della Circonferenza nei Diversi Casi
4) Posizione di un Punto Rispetto alla Circonferenza
5) Esercizi Risolti per Tutti i Livelli
6) Conclusioni
Introduzione
L'equazione della circonferenza è uno dei concetti più importanti della geometria analitica. In questa guida partiremo dalle basi e arriveremo a concetti avanzati, arricchendo il tutto con esercizi risolti per tutti i livelli.
Definizione della Circonferenza
Una circonferenza è il luogo geometrico dei punti equidistanti da un punto fisso chiamato centro.
Se il centro è C(h, k) e il raggio è r, la circonferenza è definita dalla relazione:
√(x − h)2 + (y − k)2 = r
Elevando al quadrato entrambi i membri, otteniamo l'equazione canonica della circonferenza:
(x − h)2 + (y − k)2 = r2
Equazione della Circonferenza nei Diversi Casi
Caso 1: Circonferenza con Centro nell'Origine
Se il centro è l'origine (0,0), l'equazione si semplifica in: x2 + y2 = r2
Esempio: Se r = 5, l'equazione diventa: x2 + y2 = 25
Caso 2: Circonferenza con Centro Generico C(h, k)
Per una circonferenza con centro in un punto qualsiasi (h, k) e raggio r, l'equazione generale è:
(x − h)2 + (y − k)2 = r2
Esempio: Se il centro è (3, −2) e il raggio r = 4, allora: (x − 3)2 + (y − 2)2 = 16
Caso 3: Equazione Generale della Circonferenza
Molte volte l'equazione della circonferenza appare in forma espansa:
x2 + y2 + Ax + By + C = 0
Questa forma si ottiene espandendo l'equazione canonica.
Come trovare il centro e il raggio?
Per passare dalla forma generale alla forma canonica, completiamo il quadrato.
Esempio: Data l'equazione x2 + y2 - 6x + 8y - 11 = 0
completiamo il quadrato:
1) Raggruppiamo x e y:
(x2 - 6x) + (y2 + 8y) = 11
2) Completiamo il quadrato:
(x - 3)2 - 9 + (y + 4)2 - 16 = 11
(x - 3)2 + (y + 4)2 = 36
Centro: (3, −4), Raggio: r = 6
Posizione di un Punto Rispetto alla Circonferenza
Per capire se un punto P(x0, y0) appartiene, è interno o esterno alla circonferenza, basta sostituire le coordinate nell'equazione e confrontare il risultato con r2.
Se (x0 − h)2 + (y0 − k)2 = r2 -> il punto appartiene alla circonferenza.
Se (x0 − h)2 + (y0 − k)2 < r2 -> il punto è interno.
Se (x0 − h)2 + (y0 − k)2 > r2 -> il punto è esterno.
Esempio: Data la circonferenza (x − 2)2 + (y + 1)2 = 25, il punto P(6, 2) è interno, esterno o sulla circonferenza?
(6 − 2)2 + (2 + 1)2 = 42 + 32 = 16 + 9 = 25
Il punto appartiene alla circonferenza!
Esercizi Risolti per Tutti i Livelli
Esercizio 1 - Determinare l'Equazione della Circonferenza (Base)
Trova l'equazione della circonferenza con centro (4, −3) e raggio 5.
Soluzione:
Usando la formula:
(x − 4)2 + (y + 3)2 = 52 (x − 4)2 + (y + 3)2 = 25
Esercizio 2 - Determinare Centro e Raggio (Intermedio)
Quali sono centro e raggio della circonferenza con equazione:
x2 + y2 - 10x + 4y + 20 = 0
Soluzione:
Completiamo il quadrato.
(x2 − 10x) + (y2 + 4y) = 20
Aggiungiamo i termini mancanti:
(x − 5)2 - 25 + (y + 2)2 - 4 = -20
(x − 5)2 + (y + 2)2 = 9
Centro: (5, −2), Raggio: 3
Esercizio 3 - Posizione di una Retta rispetto alla Circonferenza (Avanzato)
La retta y = 2x − 1 interseca la circonferenza x2 + y2 − 4x − 6y + 9 = 0?
Soluzione:
Sostituiamo y = 2x − 1 nell'equazione della circonferenza e risolviamo.
x2 + (2x − 1)2 - 4x - 6(2x - 1) + 9 = 0
x2 + 4x2 - 4x + 1 - 4x - 12x + 6 + 9 = 0
5x2 - 20x + 16 = 0
Troviamo il discriminante:
Δ = (-20)2 - 4(5)(16) = 400 - 320 = 80
Poiché Δ > 0, la retta interseca la circonferenza in due punti!
Conclusioni
Ora conosci tutto sull'equazione della circonferenza, dalle basi alle applicazioni avanzate!
Se vuoi mettere alla prova le tue abilità, prova a risolvere nuovi problemi e continua ad approfondire la geometria analitica.
Fonti: libri scolastici superiori
admin: 
Caldo69: 
asdasdasd: 
Isometrie e similitudini - teoria esercizi e applicazioni
Introduzione alla geometria euclidea - teoria esercizi e approfondimenti
Guida ai prodotti notevoli - teoria esercizi e applicazioni
Alla scoperta delle disequazioni di primo grado - teoria ed esercizi
Alla scoperta delle equazioni di primo grado - teoria ed esercizi
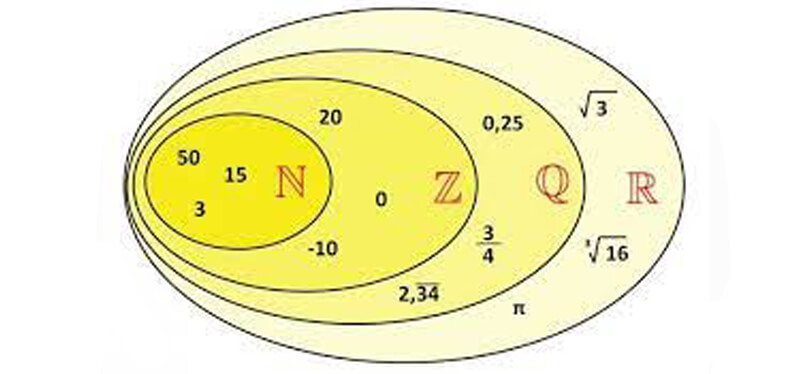Numeri irrazionali - dalla teoria agli esercizi pratici
Alla scoperta dei numeri primi - dalla teoria agli esercizi pratici
Il teorema di ruffini - dalla teoria alla pratica
Alla scoperta delle potenze - dalle basi agli esercizi avanzati
Il teorema di pitagora - dalla teoria alla pratica
Parafrasi e analisi - divina commedia - paradiso - canto XXXIII di dante alighieri