Alla Scoperta dei Numeri Primi: Dalla Teoria agli Esercizi Pratici

1) Introduzione
2) Video Riassuntivo
3) Cosa Sono i Numeri Primi?
4) Proprietà Fondamentali e Applicazioni
5) Esercizi Pratici: Dal Principiante all'Esperto
6) Curiosità e Applicazioni
7) Conclusioni
Introduzione
I numeri primi sono i mattoni fondamentali della teoria dei numeri e hanno affascinato matematici e appassionati per secoli. Che tu sia un principiante che si avvicina per la prima volta al concetto di "numero primo" oppure un esperto in cerca di nuove sfide, questo articolo ti offrirà una panoramica completa, esercizi pratici e, per soddisfare la curiosità di chi ama i dettagli, una tabella interattiva con i primi 5000 numeri primi.
Video Riassuntivo
Cosa Sono i Numeri Primi?
Un numero primo è un numero intero maggiore di 1 che ha esattamente due divisori: 1 e se stesso. In altre parole, un numero primo non può essere scomposto in un prodotto di numeri più piccoli (oltre ai triviali 1 e il numero stesso).
Esempi:
2 è il più piccolo numero primo ed è l'unico numero primo pari.
3, 5, 7, 11, 13, 17... sono altri esempi di numeri primi.
Curiosità:
I numeri primi sono infiniti, come dimostrato già da Euclide.
Essi giocano un ruolo cruciale nella crittografia moderna e in molte applicazioni informatiche.
Proprietà Fondamentali e Applicazioni
Proprietà dei Numeri Primi
Unicità della Fattorizzazione: Ogni numero intero maggiore di 1 può essere espresso in modo unico (a meno dell'ordine) come prodotto di numeri primi. Questo è il contenuto del Teorema Fondamentale dell'Aritmetica.
Distribuzione Irregolare: Non esiste una regola semplice che generi tutti i numeri primi; la loro distribuzione diventa sempre più sparsa man mano che i numeri aumentano.
Applicazioni Pratiche:
Crittografia: I numeri primi sono alla base degli algoritmi di cifratura, come RSA.
Teoria dei Numeri: Essi sono essenziali per comprendere le strutture matematiche e per risolvere problemi complessi.
Algoritmi e Calcolo: La ricerca dei numeri primi ha portato allo sviluppo di algoritmi come il Crivello di Eratostene.
Esercizi Pratici: Dalle Basi agli Approfondimenti
Esercizio 1: Verifica di un Numero Primo
Problema:
Verifica se il numero 29 è un numero primo.
Svolgimento:
Si controlla se 29 è divisibile per qualche numero compreso tra 2 e la radice quadrata di 29 (~5,39).
29 ÷ 2 = 14.5 (non intero)
29 ÷ 3 ~ 9.67 (non intero)
29 ÷ 4 = 7.25 (non intero)
29 ÷ 5 = 5.8 (non intero)
Risultato:
Poiché 29 non è divisibile per nessuno di questi numeri, è un numero primo.
Esercizio 2: Fattorizzazione in Numeri Primi
Problema:
Scomponi il numero 84 in fattori primi.
Svolgimento:
Dividiamo 84 per il più piccolo numero primo, 2:
84 ÷ 2 = 42
Dividiamo 42 per 2:
42 ÷ 2 = 21
21 non è divisibile per 2, proviamo con 3:
21 ÷ 3 = 7
Il numero 7 è un numero primo.
Risultato:
84 = 2 × 2 × 3 × 7 = 22 × 3 × 7
Esercizio 3: Problema Avanzato
Problema:
Trova la somma dei primi 10 numeri primi.
Svolgimento:
I primi 10 numeri primi sono: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29.
Calcoliamo la somma: 2 + 3 + 5 + 7 + 11 + 13 + 17 + 19 + 23 + 29 = 129
Risultato:
La somma è 129.
Tabella Interattiva dei Primi 5000 Numeri Primi
Conclusioni
I numeri primi sono elementi affascinanti e fondamentali della matematica, che offrono spunti di riflessione sia per chi si avvicina ora allo studio della matematica sia per chi desidera approfondire argomenti avanzati. Attraverso esercizi pratici e applicazioni reali, abbiamo esplorato il concetto di numero primo, la sua importanza e la sua utilità in vari campi.
Inoltre, grazie alla tabella interattiva fornita, potrai esplorare un'ampia gamma di numeri primi in modo dinamico e divertente, rendendo lo studio della matematica ancora più coinvolgente.
Buono studio e continua a esplorare l'universo affascinante dei numeri primi!
Fonti: libri scolastici superiori

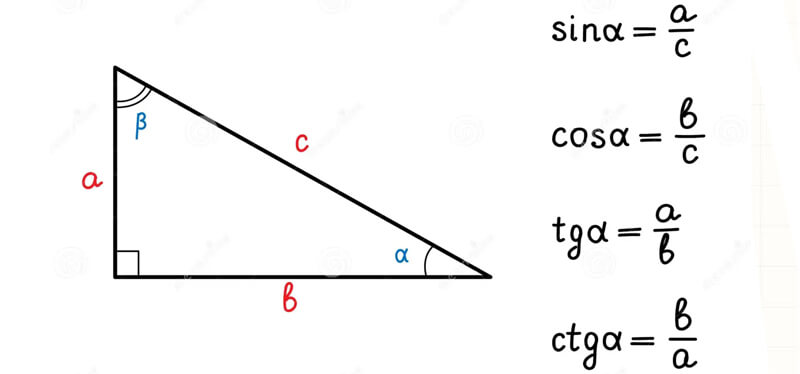 Identita trigonometriche - guida completa con esercizi risolti
Identita trigonometriche - guida completa con esercizi risolti
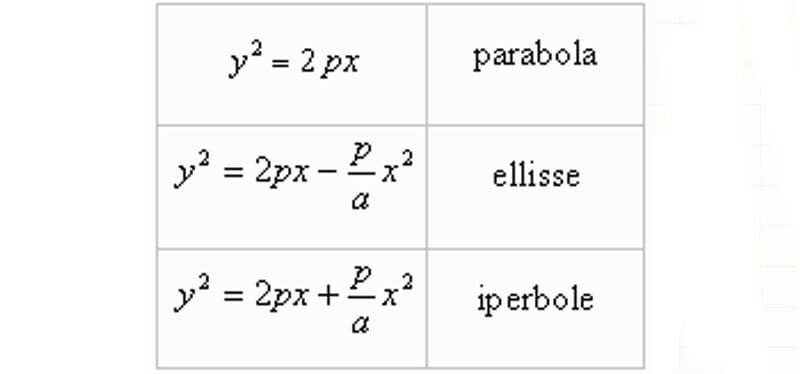 Equazione della parabola ellisse e iperbole - guida completa con esercizi risolti
Equazione della parabola ellisse e iperbole - guida completa con esercizi risolti
 Equazione della circonferenza - guida completa con esercizi risolti
Equazione della circonferenza - guida completa con esercizi risolti
 Logaritmi ed esponenziali - guida completa con esercizi risolti
Logaritmi ed esponenziali - guida completa con esercizi risolti
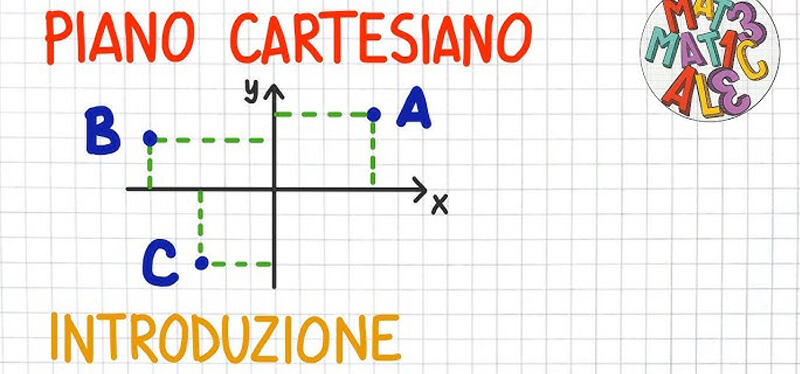 Il piano cartesiano - guida completa con esercizi risolti
Il piano cartesiano - guida completa con esercizi risolti
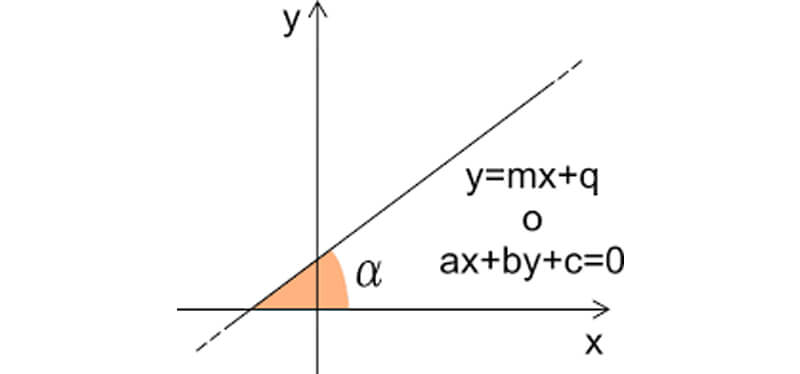 La retta - equazione e coefficiente angolare - guida completa con esercizi risolti
La retta - equazione e coefficiente angolare - guida completa con esercizi risolti
 Teorema dei seni e teorema del coseno - guida completa con esercizi risolti
Teorema dei seni e teorema del coseno - guida completa con esercizi risolti
 Seno coseno e tangente - guida completa con esercizi risolti
Seno coseno e tangente - guida completa con esercizi risolti
 Radicali e numeri complessi - guida completa con esercizi risolti
Radicali e numeri complessi - guida completa con esercizi risolti
 Guida completa alle disequazioni di secondo grado - teoria esercizi e approfondimenti
Guida completa alle disequazioni di secondo grado - teoria esercizi e approfondimenti
 Guida completa alle equazioni di secondo grado - teoria esercizi e aprofondimenti
Guida completa alle equazioni di secondo grado - teoria esercizi e aprofondimenti
 Guida completa al calcolo delle probabilita - teoria esercizi e approfondimenti
Guida completa al calcolo delle probabilita - teoria esercizi e approfondimenti
 Media moda e mediana - la statistica per tutti
Media moda e mediana - la statistica per tutti
 Le funzioni in matematica - guida completa con esercizi per tutti i livelli
Le funzioni in matematica - guida completa con esercizi per tutti i livelli
 Isometrie e similitudini - teoria esercizi e applicazioni
Isometrie e similitudini - teoria esercizi e applicazioni
 Introduzione alla geometria euclidea - teoria esercizi e approfondimenti
Introduzione alla geometria euclidea - teoria esercizi e approfondimenti
 Guida ai prodotti notevoli - teoria esercizi e applicazioni
Guida ai prodotti notevoli - teoria esercizi e applicazioni
 Alla scoperta delle disequazioni di primo grado - teoria ed esercizi
Alla scoperta delle disequazioni di primo grado - teoria ed esercizi
 Alla scoperta delle equazioni di primo grado - teoria ed esercizi
Alla scoperta delle equazioni di primo grado - teoria ed esercizi
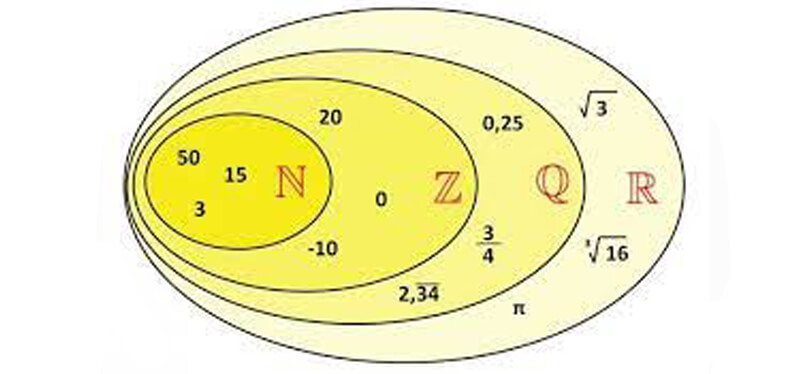 Numeri irrazionali - dalla teoria agli esercizi pratici
Numeri irrazionali - dalla teoria agli esercizi pratici