Il Teorema di Pitagora: dalla Teoria alla Pratica
1) Introduzione
2) Video Riassuntivo
3) Teoria
4) Spiegazione Base e Contesto Storico
5) Esercizi Pratici: Dal Principiante all'Esperto
6) Curiosità e Applicazioni
7) Domande Frequenti
8) Conclusioni
Introduzione
Il teorema di Pitagora è uno dei pilastri della geometria e un concetto fondamentale in matematica. Che tu sia un neofita che si avvicina per la prima volta al mondo dei triangoli rettangoli o un esperto in cerca di esercizi stimolanti, questo articolo ti guiderà attraverso spiegazioni chiare, esempi pratici ed esercizi passo-passo.
Video Riassuntivo
Teoria
Introduzione
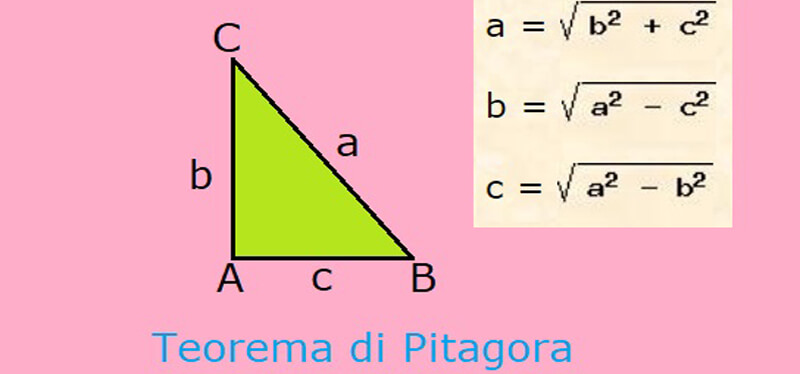
Il teorema di Pitagora afferma che, in un triangolo rettangolo, il quadrato dell'ipotenusa (il lato opposto all'angolo retto) è uguale alla somma dei quadrati dei due cateti. In formula:
a2 + b2 = c2
Dove:
a e b sono le lunghezze dei cateti;
c è la lunghezza dell'ipotenusa.
Questa semplice relazione ha implicazioni enormi: non solo è uno strumento indispensabile per risolvere problemi geometrici, ma ha anche applicazioni in fisica, ingegneria, informatica e molti altri campi.
Spiegazione Base e Contesto Storico
Il Contesto Storico
Il teorema prende il nome dal filosofo e matematico greco Pitagora, vissuto nel VI secolo a.C. Sebbene la conoscenza di rapporti simili tra i lati dei triangoli esista già in altre culture, Pitagora e i suoi discepoli furono tra i primi a formalizzare e dimostrare rigorosamente questo principio.
Concetti di Base
Triangolo rettangolo: Un triangolo in cui uno degli angoli è retto (90°).
Cateti: I due lati che formano l'angolo retto.
Ipotenusa: Il lato opposto all'angolo retto, il più lungo del triangolo.
Per chi si avvicina alla matematica, è importante visualizzare il triangolo rettangolo. Immagina un triangolo con due lati perpendicolari: i quadrati costruiti su questi lati hanno aree che, sommate, sono uguali all'area del quadrato costruito sull'ipotenusa.
Esercizi Pratici: Dal Principiante all'Esperto
Esercizio 1: Calcolo dell'Ipotenusa
Problema:
In un triangolo rettangolo, i cateti misurano 3 e 4 unità. Calcola la lunghezza dell'ipotenusa.
Svolgimento:
Utilizziamo il teorema:
a2 + b2 = c2
32 + 42 = c2
9 + 16 = c2
25 = c2
c = √25 = 5
Risultato:
L'ipotenusa misura 5 unità.
Esercizio 2: Verifica di un Triangolo Rettangolo
Problema:
Verifica se un triangolo con lati di lunghezza 5, 12 e 13 è rettangolo.
Svolgimento:
Verifichiamo se la relazione del teorema è soddisfatta:
52 + 122 = 25 + 144 = 169
132 = 169
Risultato:
Poiché 25 + 144 = 169, il triangolo è rettangolo.
Esercizio 3: Problema Avanzato
Problema:
In un triangolo rettangolo, la somma dei cateti è pari a 14 unità e l'ipotenusa misura 10 unità. Trova le lunghezze dei cateti.
Svolgimento:
Sia a e b i cateti. Abbiamo:
a + b = 14
a2 + b2 = 102 = 100
Utilizziamo l'identità:(a + b)2 = a2 + 2ab + b2
Quindi:142 = 100 + 2ab
196 = 100 + 2ab
2ab = 96
ab = 48
Ora, i cateti sono le soluzioni dell'equazione quadratica:x2 – (a + b)x + ab = 0
x2 – 14x + 48 = 0
Calcoliamo il discriminante:
Δ = 142 – 4 · 1 · 48 = 196 – 192 = 4
Quindi:x = (14 ± √4) / 2 = (14 ± 2) / 2
Otteniamo:
x1 = (14 + 2) / 2 = 8
x2 = (14 – 2) / 2 = 6
Risultato:
I cateti misurano 6 e 8 unità.
Curiosità e Applicazioni
Numeri Pitagorici:
Esistono interi che soddisfano il teorema, come il celebre 3-4-5 o il 5-12-13. Questi insiemi vengono chiamati "triple pitagoriche" e hanno affascinato matematici per secoli.
Applicazioni nel Mondo Reale:
Il teorema non è solo un concetto astratto: viene utilizzato nella progettazione di edifici, nella navigazione, nella grafica computerizzata e persino nella tecnologia GPS.
Per chi desidera approfondire ulteriormente, è possibile:
Esplorare la dimostrazione geometrica e quella algebrica del teorema.
Analizzare il teorema inverso di Pitagora, che permette di verificare se un triangolo è rettangolo.
Studiare le generalizzazioni del teorema in spazi non euclidei o in dimensioni superiori.
Domande Frequenti
1. Il teorema di Pitagora vale per tutti i triangoli?
No, si applica esclusivamente ai triangoli rettangoli.
2. È possibile avere triangoli con cateti e ipotenusa interi?
Sì, esistono infiniti insiemi di numeri interi (triple pitagoriche) che soddisfano il teorema.
3. Come posso dimostrare il teorema?
Esistono numerose dimostrazioni, sia geometriche che algebriche. Una delle più classiche prevede la costruzione di quadrati sui lati del triangolo e la dimostrazione dell'uguaglianza delle aree.
Conclusioni
Il teorema di Pitagora è molto più di una semplice formula: è una porta d'accesso a un universo di applicazioni pratiche e teorie matematiche. Sia che tu stia muovendo i primi passi nello studio della geometria o che tu stia cercando di approfondire concetti avanzati, il teorema offre spunti e sfide a ogni livello di competenza. Continuare a esplorare, esercitarsi e cercare nuove applicazioni ti permetterà di apprezzare ancora di più questo caposaldo della matematica.
Buono studio e buona pratica!
Fonti: libri scolastici superiori

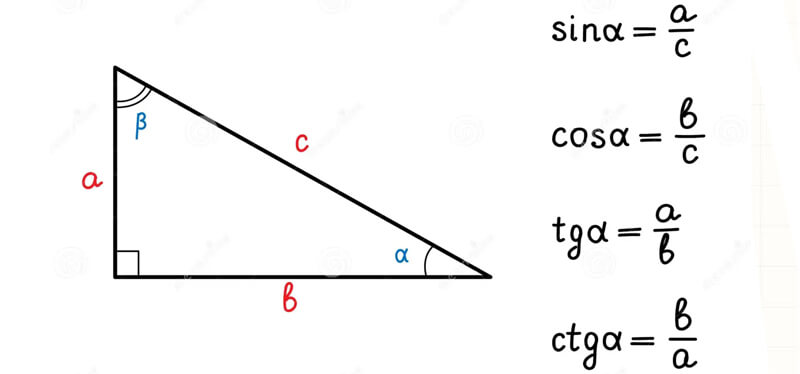 Identita trigonometriche - guida completa con esercizi risolti
Identita trigonometriche - guida completa con esercizi risolti
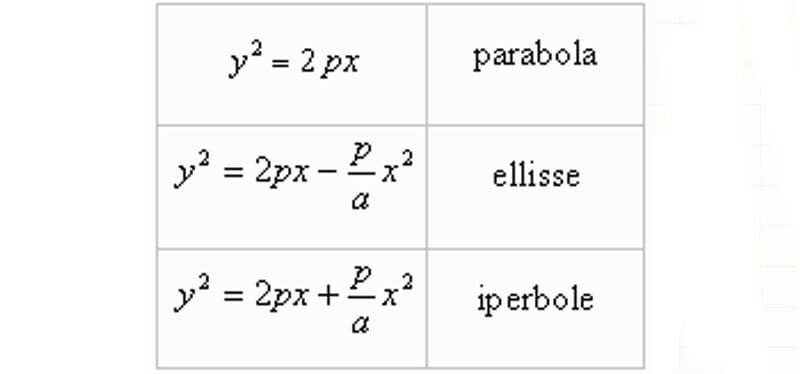 Equazione della parabola ellisse e iperbole - guida completa con esercizi risolti
Equazione della parabola ellisse e iperbole - guida completa con esercizi risolti
 Equazione della circonferenza - guida completa con esercizi risolti
Equazione della circonferenza - guida completa con esercizi risolti
 Logaritmi ed esponenziali - guida completa con esercizi risolti
Logaritmi ed esponenziali - guida completa con esercizi risolti
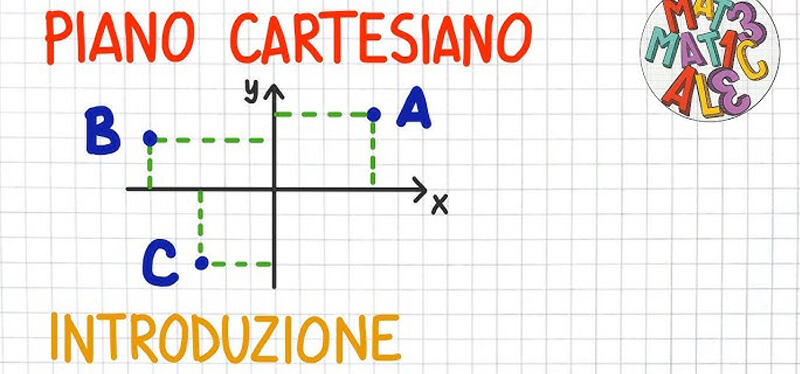 Il piano cartesiano - guida completa con esercizi risolti
Il piano cartesiano - guida completa con esercizi risolti
 La retta - equazione e coefficiente angolare - guida completa con esercizi risolti
La retta - equazione e coefficiente angolare - guida completa con esercizi risolti
 Teorema dei seni e teorema del coseno - guida completa con esercizi risolti
Teorema dei seni e teorema del coseno - guida completa con esercizi risolti
 Seno coseno e tangente - guida completa con esercizi risolti
Seno coseno e tangente - guida completa con esercizi risolti
 Radicali e numeri complessi - guida completa con esercizi risolti
Radicali e numeri complessi - guida completa con esercizi risolti
 Guida completa alle disequazioni di secondo grado - teoria esercizi e approfondimenti
Guida completa alle disequazioni di secondo grado - teoria esercizi e approfondimenti
 Guida completa alle equazioni di secondo grado - teoria esercizi e aprofondimenti
Guida completa alle equazioni di secondo grado - teoria esercizi e aprofondimenti
 Guida completa al calcolo delle probabilita - teoria esercizi e approfondimenti
Guida completa al calcolo delle probabilita - teoria esercizi e approfondimenti
 Media moda e mediana - la statistica per tutti
Media moda e mediana - la statistica per tutti
 Le funzioni in matematica - guida completa con esercizi per tutti i livelli
Le funzioni in matematica - guida completa con esercizi per tutti i livelli
 Isometrie e similitudini - teoria esercizi e applicazioni
Isometrie e similitudini - teoria esercizi e applicazioni
 Introduzione alla geometria euclidea - teoria esercizi e approfondimenti
Introduzione alla geometria euclidea - teoria esercizi e approfondimenti
 Guida ai prodotti notevoli - teoria esercizi e applicazioni
Guida ai prodotti notevoli - teoria esercizi e applicazioni
 Alla scoperta delle disequazioni di primo grado - teoria ed esercizi
Alla scoperta delle disequazioni di primo grado - teoria ed esercizi
 Alla scoperta delle equazioni di primo grado - teoria ed esercizi
Alla scoperta delle equazioni di primo grado - teoria ed esercizi
 Numeri irrazionali - dalla teoria agli esercizi pratici
Numeri irrazionali - dalla teoria agli esercizi pratici